Refine listing
Actions for selected content:
279 results in 20Gxx
On the action of the unitary group on the projective plane over a local field
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 62 / Issue 3 / June 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 371-397
- Print publication:
- June 1997
-
- Article
-
- You have access
- Export citation
Commutators in pseudo-orthogonal groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 3 / December 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 353-365
- Print publication:
- December 1995
-
- Article
-
- You have access
- Export citation
On the faithful representations, of degree 2n, of certain extensions of 2-groups by orthogonal and symplectic groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 2 / April 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 232-247
- Print publication:
- April 1995
-
- Article
-
- You have access
- Export citation
On flag varieties, hyperplane complements and Springer representations of Weyl groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 3 / December 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 449-485
- Print publication:
- December 1990
-
- Article
-
- You have access
- Export citation
On presentation of PSL (2, pn)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 48 / Issue 2 / April 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 333-346
- Print publication:
- April 1990
-
- Article
-
- You have access
- Export citation
Maps into Dynkin diagrams arising from regular monoids
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 2 / October 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 313-321
- Print publication:
- October 1989
-
- Article
-
- You have access
- Export citation
A filtration of Weyl modules for large weights
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 45 / Issue 2 / October 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 187-194
- Print publication:
- October 1988
-
- Article
-
- You have access
- Export citation
Representations of minimally almost periodic groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 3 / December 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 366-375
- Print publication:
- December 1986
-
- Article
-
- You have access
- Export citation
Nilpotent orbits of exceptional Lie algebras over algebraically closed fields of bad characteristic
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 38 / Issue 3 / June 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 330-350
- Print publication:
- June 1985
-
- Article
-
- You have access
- Export citation
The p-periodicity of the groups GL (n, Os(K)) and SL(n, Os(K))
- Part of
-
- Journal:
- Mathematika / Volume 31 / Issue 1 / June 1984
- Published online by Cambridge University Press:
- 26 February 2010, pp. 89-97
- Print publication:
- June 1984
-
- Article
- Export citation
Abelian 2-subgroups of finite symplectic groups in characteristic 2
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 33 / Issue 3 / December 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 345-350
- Print publication:
- December 1982
-
- Article
-
- You have access
- Export citation
Abelian Unipotent Subgroups of Finite Unitary and Symplectic Groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 33 / Issue 3 / December 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 331-344
- Print publication:
- December 1982
-
- Article
-
- You have access
- Export citation
Abelian unipotent subgroups of finite orthogonal groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 32 / Issue 2 / April 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 223-245
- Print publication:
- April 1982
-
- Article
-
- You have access
- Export citation
Trace polynomials of words in special linear groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 28 / Issue 4 / December 1979
- Published online by Cambridge University Press:
- 09 April 2009, pp. 401-412
- Print publication:
- December 1979
-
- Article
-
- You have access
- Export citation
Permutation characters of finite groups of Lie type
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 27 / Issue 3 / May 1979
- Published online by Cambridge University Press:
- 09 April 2009, pp. 378-384
- Print publication:
- May 1979
-
- Article
-
- You have access
- Export citation
A note on the conjugacy of Cartan subalgebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 27 / Issue 2 / March 1979
- Published online by Cambridge University Press:
- 09 April 2009, pp. 163-166
- Print publication:
- March 1979
-
- Article
-
- You have access
- Export citation
Large abelian subgroups of Chevalley groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 27 / Issue 1 / February 1979
- Published online by Cambridge University Press:
- 09 April 2009, pp. 59-87
- Print publication:
- February 1979
-
- Article
-
- You have access
- Export citation
Existence of finite groups with classical commutator subgroup
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 25 / Issue 1 / February 1978
- Published online by Cambridge University Press:
- 09 April 2009, pp. 41-44
- Print publication:
- February 1978
-
- Article
-
- You have access
- Export citation
Projective representations of the infinite orthogonal group
- Part of
-
- Journal:
- Mathematika / Volume 24 / Issue 1 / June 1977
- Published online by Cambridge University Press:
- 26 February 2010, pp. 115-121
- Print publication:
- June 1977
-
- Article
- Export citation
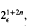 , or to the central product 4 o 2
, or to the central product 4 o 2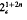 and powers of
and powers of 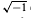 otherwise. This explicit description of a projective representation is useful for computing character values or computing with central extensions of
otherwise. This explicit description of a projective representation is useful for computing character values or computing with central extensions of 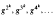 for some positive integer
for some positive integer  . In this paper Ab(
. In this paper Ab(