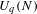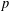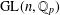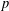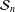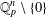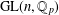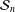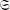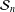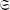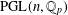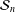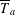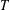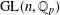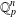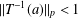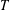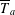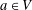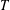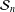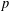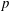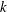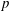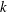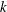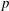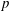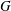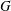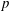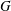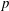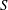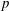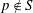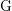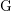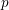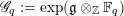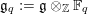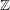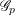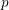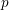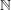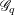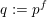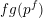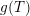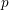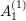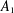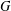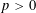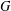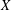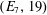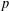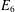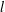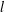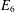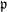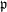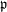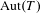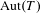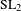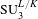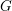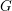Refine listing
Actions for selected content:
279 results in 20Gxx
BOREL DENSITY FOR APPROXIMATE LATTICES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 05 November 2019, e40
-
- Article
-
- You have access
- Open access
- Export citation
QUANTUM INCREASING SEQUENCES GENERATE QUANTUM PERMUTATION GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 27 September 2019, pp. 631-639
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
Type classification of extreme quantized characters
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 06 September 2019, pp. 593-605
- Print publication:
- February 2021
-
- Article
- Export citation
DISTALITY OF CERTAIN ACTIONS ON
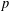 $p$-ADIC SPHERES
$p$-ADIC SPHERES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 29 July 2019, pp. 250-261
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
Retract Rationality and Algebraic Tori
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 18 July 2019, pp. 173-186
- Print publication:
- March 2020
-
- Article
-
- You have access
- Export citation
Kirillov’s orbit method and polynomiality of the faithful dimension of
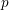 $p$-groups
$p$-groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 8 / August 2019
- Published online by Cambridge University Press:
- 11 July 2019, pp. 1618-1654
- Print publication:
- August 2019
-
- Article
- Export citation
Affine cluster monomials are generalized minors
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 7 / July 2019
- Published online by Cambridge University Press:
- 14 June 2019, pp. 1301-1326
- Print publication:
- July 2019
-
- Article
- Export citation
Martin boundaries of the duals of free unitary quantum groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 6 / June 2019
- Published online by Cambridge University Press:
- 31 May 2019, pp. 1171-1193
- Print publication:
- June 2019
-
- Article
- Export citation
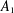 $A_{1}$-TYPE SUBGROUPS CONTAINING REGULAR UNIPOTENT ELEMENTS
$A_{1}$-TYPE SUBGROUPS CONTAINING REGULAR UNIPOTENT ELEMENTS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 24 April 2019, e12
-
- Article
-
- You have access
- Open access
- Export citation
CENTRALIZERS OF p-SUBGROUPS IN SIMPLE LOCALLY FINITE GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 21 February 2019, pp. 183-186
- Print publication:
- January 2020
-
- Article
-
- You have access
- Open access
- Export citation
COMPATIBLE SYSTEMS OF GALOIS REPRESENTATIONS ASSOCIATED TO THE EXCEPTIONAL GROUP
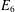 $E_{6}$
$E_{6}$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 06 February 2019, e4
-
- Article
-
- You have access
- Open access
- Export citation
Local duality for representations of finite group schemes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 2 / February 2019
- Published online by Cambridge University Press:
- 18 February 2019, pp. 424-453
- Print publication:
- February 2019
-
- Article
-
- You have access
- HTML
- Export citation
ON THE NUMBER OF REAL CLASSES IN THE FINITE PROJECTIVE LINEAR AND UNITARY GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 31 January 2019, pp. 93-107
- Print publication:
- January 2020
-
- Article
-
- You have access
- Export citation
A New Axiomatics for Masures
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 732-773
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
Induction for locally compact quantum groups revisited
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 1071-1093
- Print publication:
- April 2020
-
- Article
- Export citation
The Structure of Root Data and Smooth Regular Embeddings of Reductive Groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 29 November 2018, pp. 523-552
-
- Article
- Export citation
PRESENTATIONS OF AFFINE KAC–MOODY GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 26 October 2018, e21
-
- Article
-
- You have access
- Open access
- Export citation
Springer correspondence for the split symmetric pair in type
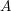 $A$
$A$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 11 / November 2018
- Published online by Cambridge University Press:
- 11 October 2018, pp. 2403-2425
- Print publication:
- November 2018
-
- Article
- Export citation
CHABAUTY LIMITS OF ALGEBRAIC GROUPS ACTING ON TREES THE QUASI-SPLIT CASE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 06 August 2018, pp. 1031-1091
- Print publication:
- July 2020
-
- Article
- Export citation
INTERTWINING SEMISIMPLE CHARACTERS FOR
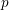 $p$-ADIC CLASSICAL GROUPS
$p$-ADIC CLASSICAL GROUPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 238 / June 2020
- Published online by Cambridge University Press:
- 16 July 2018, pp. 137-205
- Print publication:
- June 2020
-
- Article
-
- You have access
- HTML
- Export citation