 $q$-SCHUR ALGEBRAS AND
$q$-SCHUR ALGEBRAS AND  $q$-SCHUR DUALITIES OF FINITE TYPE
$q$-SCHUR DUALITIES OF FINITE TYPE
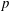 $p$-rank
$p$-rank
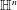 $\mathbb{H}^{n}$ and Covolumes of Higher Dimensional Modular Groups
$\mathbb{H}^{n}$ and Covolumes of Higher Dimensional Modular Groups
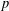 $p$-GROUPS WITH AUTOMORPHISM GROUPS RELATED TO THE CHEVALLEY GROUP
$p$-GROUPS WITH AUTOMORPHISM GROUPS RELATED TO THE CHEVALLEY GROUP 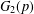 $G_{2}(p)$
$G_{2}(p)$
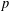 $p$-ADIC SPHERES
$p$-ADIC SPHERES
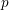 $p$-groups
$p$-groups
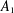 $A_{1}$-TYPE SUBGROUPS CONTAINING REGULAR UNIPOTENT ELEMENTS
$A_{1}$-TYPE SUBGROUPS CONTAINING REGULAR UNIPOTENT ELEMENTS