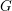 $G$-BASES
$G$-BASES
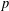 $p$
$p$
 $1$
$1$
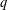 $q$-ROOK MONOID ALGEBRA
$q$-ROOK MONOID ALGEBRA
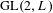 $\text{GL}(2,L)$ VIA SEMISTABLE MODELS OF
$\text{GL}(2,L)$ VIA SEMISTABLE MODELS OF 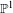 $\mathbb{P}^{1}$
$\mathbb{P}^{1}$
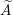 $\widetilde{A}$
$\widetilde{A}$
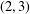 $(2,3)$ -GENERATION OF THE SPECIAL LINEAR GROUPS OVER FINITE FIELDS
$(2,3)$ -GENERATION OF THE SPECIAL LINEAR GROUPS OVER FINITE FIELDS