Refine listing
Actions for selected content:
279 results in 20Gxx
Shifted generic cohomology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 10 / October 2013
- Published online by Cambridge University Press:
- 07 August 2013, pp. 1765-1788
- Print publication:
- October 2013
-
- Article
- Export citation
Unipotent differential algebraic groups as parameterized differential Galois groups
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 4 / October 2014
- Published online by Cambridge University Press:
- 18 July 2013, pp. 671-700
- Print publication:
- October 2014
-
- Article
- Export citation
On the symbol length of
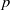 $p$-algebras
$p$-algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 8 / August 2013
- Published online by Cambridge University Press:
- 22 May 2013, pp. 1353-1363
- Print publication:
- August 2013
-
- Article
- Export citation
TILING BRANCHING MULTIPLICITY SPACES WITH GL
 ${}_{2} $ PATTERN BLOCKS
${}_{2} $ PATTERN BLOCKS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 10 April 2013, pp. 362-374
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
Koszul, Ringel and Serre duality for strict polynomial functors
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 6 / June 2013
- Published online by Cambridge University Press:
- 18 March 2013, pp. 996-1018
- Print publication:
- June 2013
-
- Article
- Export citation
A fiber dimension theorem for essential and canonical dimension
- Part of
-
- Journal:
- Compositio Mathematica / Volume 149 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 04 December 2012, pp. 148-174
- Print publication:
- January 2013
-
- Article
- Export citation
Algorithmic construction of Chevalley bases
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 December 2012, pp. 436-443
-
- Article
-
- You have access
- Export citation
Commuting elements in central products of special unitary groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 24 October 2012, pp. 1-12
-
- Article
-
- You have access
- Export citation
ALGORITHMS TO IDENTIFY ABUNDANT p-SINGULAR ELEMENTS IN FINITE CLASSICAL GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 1 / August 2012
- Published online by Cambridge University Press:
- 06 August 2012, pp. 50-63
- Print publication:
- August 2012
-
- Article
-
- You have access
- Export citation
Twisted gamma filtration of a linear algebraic group
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 5 / September 2012
- Published online by Cambridge University Press:
- 25 July 2012, pp. 1645-1654
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
ON TORSION OF CLASS GROUPS OF CM TORI
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 2 / July 2012
- Published online by Cambridge University Press:
- 28 March 2012, pp. 305-318
- Print publication:
- July 2012
-
- Article
- Export citation
Langlands duality and global Springer theory
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 3 / May 2012
- Published online by Cambridge University Press:
- 19 March 2012, pp. 835-867
- Print publication:
- May 2012
-
- Article
-
- You have access
- Export citation
Generalized affine Springer fibres
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 11 / Issue 3 / July 2012
- Published online by Cambridge University Press:
- 03 January 2012, pp. 569-609
- Print publication:
- July 2012
-
- Article
- Export citation
ON THE SUPPORT VARIETIES FOR DEMAZURE MODULES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 91 / Issue 3 / December 2011
- Published online by Cambridge University Press:
- 19 March 2012, pp. 343-363
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation
Finiteness theorems for algebraic groups over function fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 2 / March 2012
- Published online by Cambridge University Press:
- 30 November 2011, pp. 555-639
- Print publication:
- March 2012
-
- Article
-
- You have access
- Export citation
A twisted topological trace formula for Hecke operators and liftings from symplectic to general linear groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 148 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 09 November 2011, pp. 65-120
- Print publication:
- January 2012
-
- Article
-
- You have access
- Export citation
Decomposition matrices for d-Harish-Chandra series: the exceptional rank two cases
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 14 / 2011
- Published online by Cambridge University Press:
- 01 November 2011, pp. 271-290
-
- Article
-
- You have access
- Export citation
Cohomologie d’intersection des variétés modulaires de Siegel, suite
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 6 / November 2011
- Published online by Cambridge University Press:
- 28 September 2011, pp. 1671-1740
- Print publication:
- November 2011
-
- Article
-
- You have access
- Export citation
Restrictions to G(𝔽p) and G(r) of rational G-modules
- Part of
-
- Journal:
- Compositio Mathematica / Volume 147 / Issue 6 / November 2011
- Published online by Cambridge University Press:
- 26 August 2011, pp. 1955-1978
- Print publication:
- November 2011
-
- Article
-
- You have access
- Export citation
GEOMETRIC STRUCTURE IN THE TEMPERED DUAL OF SLℓ(F): TORAL CASE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 3 / December 2011
- Published online by Cambridge University Press:
- 01 August 2011, pp. 425-432
- Print publication:
- December 2011
-
- Article
-
- You have access
- Export citation

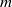
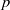
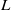
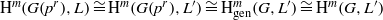
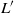
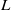
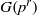
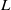
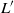
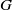
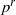
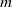
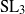
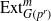
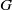
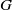
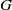
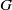
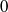
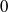
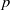
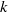
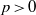
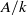
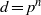
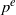
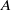
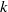
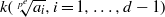
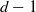
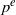

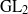
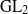
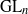
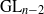
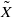 by gluing together 2
by gluing together 2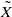 and get formulas for the traces of Hecke operators ℋ acting on the cohomology of
and get formulas for the traces of Hecke operators ℋ acting on the cohomology of 