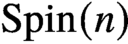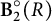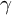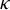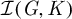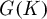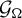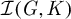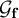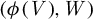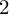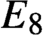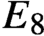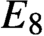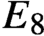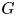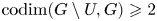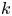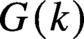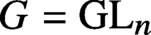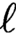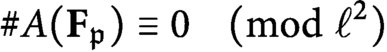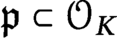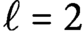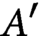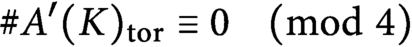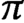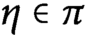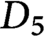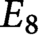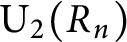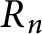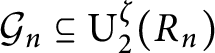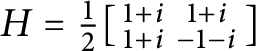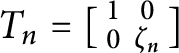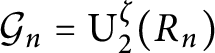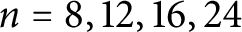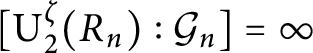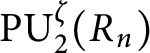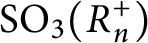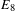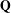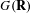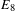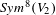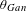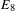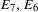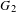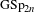Refine listing
Actions for selected content:
277 results in 20Gxx
Maximal indexes of flag varieties for spin groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 26 April 2021, e34
-
- Article
-
- You have access
- Open access
- Export citation
Explicit methods for the Hasse norm principle and applications to An and Sn extensions
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 22 April 2021, pp. 489-529
- Print publication:
- May 2022
-
- Article
-
- You have access
- Open access
- Export citation
On the Finiteness length of some soluble linear groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 21 April 2021, pp. 1209-1243
- Print publication:
- October 2022
-
- Article
- Export citation
GROUPS OF WORLDVIEW TRANSFORMATIONS IMPLIED BY EINSTEIN’S SPECIAL PRINCIPLE OF RELATIVITY OVER ARBITRARY ORDERED FIELDS
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 15 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 23 March 2021, pp. 334-361
- Print publication:
- June 2022
-
- Article
- Export citation
ON FORMAL DEGREES OF UNIPOTENT REPRESENTATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 19 March 2021, pp. 1947-1999
- Print publication:
- November 2022
-
- Article
- Export citation
THE CENTER OF SL2 TILTING MODULES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 05 March 2021, pp. 165-184
- Print publication:
- January 2022
-
- Article
- Export citation
Low-dimensional representations of finite orthogonal groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 3 / November 2021
- Published online by Cambridge University Press:
- 26 January 2021, pp. 585-606
- Print publication:
- November 2021
-
- Article
- Export citation
THÉORIE DE BRUHAT-TITS POUR LES GROUPES QUASI-RÉDUCTIFS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 25 January 2021, pp. 1331-1362
- Print publication:
- July 2022
-
- Article
- Export citation
BOUNDNESS OF INTERSECTION NUMBERS FOR ACTIONS BY TWO-DIMENSIONAL BIHOLOMORPHISMS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 22 January 2021, pp. 1677-1700
- Print publication:
- September 2022
-
- Article
- Export citation
EXTREMAL CASES OF RAPOPORT–ZINK SPACES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 20 January 2021, pp. 1727-1782
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- Export citation
A class of continuous non-associative algebras arising from algebraic groups including
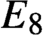 $E_8$
$E_8$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 14 January 2021, e6
-
- Article
-
- You have access
- Open access
- Export citation
LECTURES ON THE GEOMETRY AND MODULAR REPRESENTATION THEORY OF ALGEBRAIC GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 110 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 13 January 2021, pp. 1-47
- Print publication:
- February 2021
-
- Article
- Export citation
Minimal rational curves on generalized Bott–Samelson varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 15 February 2021, pp. 122-153
- Print publication:
- January 2021
-
- Article
- Export citation
Arithmetic purity of strong approximation for semi-simple simply connected groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 01 February 2021, pp. 2628-2649
- Print publication:
- December 2020
-
- Article
- Export citation
Semisimplification for subgroups of reductive algebraic groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 09 November 2020, e43
-
- Article
-
- You have access
- Open access
- Export citation
Divisibility of torsion subgroups of abelian surfaces over number fields
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 28 October 2020, pp. 266-298
- Print publication:
- February 2022
-
- Article
- Export citation
Fourier coefficients of minimal and next-to-minimal automorphic representations of simply-laced groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 21 September 2020, pp. 122-169
- Print publication:
- February 2022
-
- Article
-
- You have access
- Open access
- Export citation
The Clifford-cyclotomic group and Euler–Poincaré characteristics
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 02 September 2020, pp. 651-666
- Print publication:
- September 2021
-
- Article
- Export citation
THE MINIMAL MODULAR FORM ON QUATERNIONIC
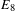 $E_{8}$
$E_{8}$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 20 August 2020, pp. 603-636
- Print publication:
- March 2022
-
- Article
- Export citation
GENERALISED QUANTUM DETERMINANTAL RINGS ARE MAXIMAL ORDERS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 04 August 2020, pp. 515-525
- Print publication:
- September 2021
-
- Article
- Export citation