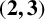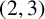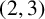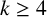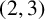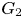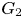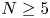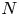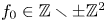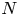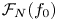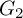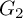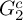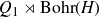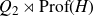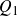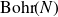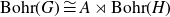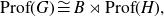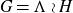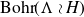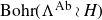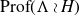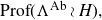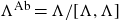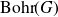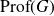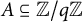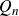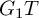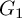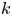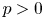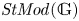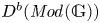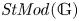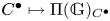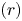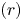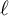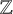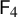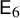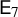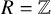Refine listing
Actions for selected content:
279 results in 20Gxx
THE
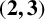 $\boldsymbol {(2,3)}$-GENERATION OF THE FINITE SIMPLE ODD-DIMENSIONAL ORTHOGONAL GROUPS
$\boldsymbol {(2,3)}$-GENERATION OF THE FINITE SIMPLE ODD-DIMENSIONAL ORTHOGONAL GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 28 February 2024, pp. 130-148
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Modular forms of half-integral weight on exceptional groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 22 February 2024, pp. 657-707
- Print publication:
- March 2024
-
- Article
- Export citation
PERFECTING GROUP SCHEMES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 16 February 2024, pp. 2549-2591
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Most odd-degree binary forms fail to primitively represent a square
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 08 February 2024, pp. 481-517
- Print publication:
- March 2024
-
- Article
- Export citation
Lie algebra actions on module categories for truncated shifted yangians
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 31 January 2024, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Joint partial equidistribution of Farey rays in negatively curved manifolds and trees
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 08 January 2024, pp. 2700-2736
- Print publication:
- September 2024
-
- Article
- Export citation
COUNTING DISCRETE, LEVEL-
 $1$, QUATERNIONIC AUTOMORPHIC REPRESENTATIONS ON
$1$, QUATERNIONIC AUTOMORPHIC REPRESENTATIONS ON 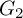 $G_2$
$G_2$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 5 / September 2024
- Published online by Cambridge University Press:
- 13 December 2023, pp. 2127-2157
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON MODEL-THEORETIC CONNECTED GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 14 November 2023, pp. 50-79
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON ENDOMORPHISMS OF EXTENSIONS IN TANNAKIAN CATEGORIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 07 November 2023, pp. 103-114
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On Bohr compactifications and profinite completions of group extensions
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 09 October 2023, pp. 373-393
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On some multiplicative properties of large difference sets
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 08 September 2023, pp. 1538-1555
- Print publication:
- October 2024
-
- Article
- Export citation
Quantum symmetries of Cayley graphs of abelian groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 12 October 2023, pp. 655-686
- Print publication:
- September 2023
-
- Article
- Export citation
Hecke category actions via Smith–Treumann theory
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 23 August 2023, pp. 2089-2124
- Print publication:
- October 2023
-
- Article
- Export citation
Connected components of affine Deligne–Lusztig varieties for unramified groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 17 August 2023, pp. 2051-2088
- Print publication:
- October 2023
-
- Article
- Export citation
Coniveau filtrations and Milnor operation
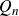 $Q_n$
$Q_n$
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 3 / November 2023
- Published online by Cambridge University Press:
- 08 May 2023, pp. 521-538
- Print publication:
- November 2023
-
- Article
- Export citation
A HECKE ACTION ON
 $G_1T$-MODULES
$G_1T$-MODULES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 28 April 2023, pp. 1125-1167
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Integration questions in separably good characteristics
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 890-932
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Support varieties and stable categories for algebraic groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 4 / April 2023
- Published online by Cambridge University Press:
- 27 March 2023, pp. 746-779
- Print publication:
- April 2023
-
- Article
- Export citation
On the primality of totally ordered q-factorization graphs
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 20 March 2023, pp. 594-637
- Print publication:
- April 2024
-
- Article
- Export citation
Albert algebras over
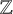 $\mathbb {Z}$ and other rings
$\mathbb {Z}$ and other rings
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 14 March 2023, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation