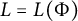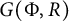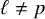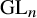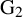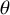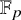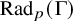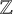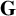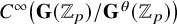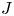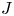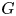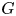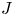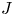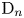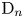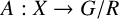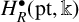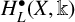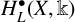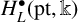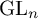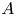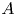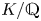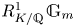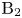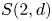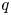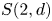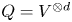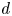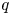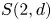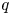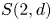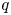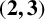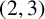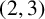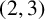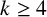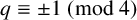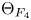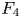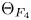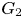Refine listing
Actions for selected content:
277 results in 20Gxx
A classification of Shimura curves in
 $ \mathscr {A}_g$
$ \mathscr {A}_g$
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 20 December 2024, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On quasi and weak Steinberg characters of general linear groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 19 December 2024, pp. 403-420
-
- Article
- Export citation
Uniform bounded elementary generation of Chevalley groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 10 December 2024, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On split quasi-hereditary covers and Ringel duality
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 02 December 2024, e105
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quantum wreath products and Schur–Weyl duality I
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 26 November 2024, e108
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lifting G-Valued Galois Representations when
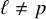 $\ell \neq p$
$\ell \neq p$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 26 November 2024, e109
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The line bundles on the moduli stack of principal bundles on families of curves
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 22 November 2024, pp. 80-127
-
- Article
- Export citation
All Kronecker coefficients are reduced Kronecker coefficients
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 18 November 2024, e22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Height functions on Hecke orbits and the generalised André–Pink–Zannier conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 19 November 2024, pp. 2531-2584
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bounds on multiplicities of symmetric pairs of finite groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 09 September 2024, e73
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The
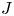 $J$-invariant over splitting fields of Tits algebras
$J$-invariant over splitting fields of Tits algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 11 September 2024, pp. 2100-2114
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
TWISTED ACTIONS ON COHOMOLOGIES AND BIMODULES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 31 May 2024, pp. 187-238
- Print publication:
- October 2024
-
- Article
- Export citation
Orthogonality relations for deep level Deligne–Lusztig schemes of Coxeter type
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 22 May 2024, e66
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ARCHIMEDEAN NEWFORM THEORY FOR
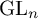 $\operatorname {\mathrm {GL}}_n$
$\operatorname {\mathrm {GL}}_n$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 17 May 2024, pp. 41-116
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Powers of commutators in linear algebraic groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 14 May 2024, pp. 830-837
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weak approximation on the norm one torus
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 06 May 2024, pp. 1304-1348
- Print publication:
- June 2024
-
- Article
- Export citation
On Donkin's tilting module conjecture II: counterexamples
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 02 May 2024, pp. 1167-1193
- Print publication:
- June 2024
-
- Article
- Export citation
Quasi-hereditary covers of Temperley–Lieb algebras and relative dominant dimension
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 April 2024, pp. 1-38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE
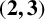 $\boldsymbol {(2,3)}$-GENERATION OF THE FINITE SIMPLE ODD-DIMENSIONAL ORTHOGONAL GROUPS
$\boldsymbol {(2,3)}$-GENERATION OF THE FINITE SIMPLE ODD-DIMENSIONAL ORTHOGONAL GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 28 February 2024, pp. 130-148
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Modular forms of half-integral weight on exceptional groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 22 February 2024, pp. 657-707
- Print publication:
- March 2024
-
- Article
- Export citation