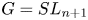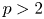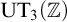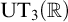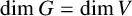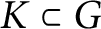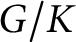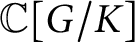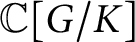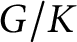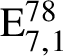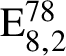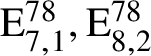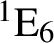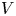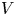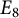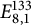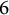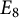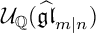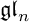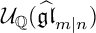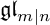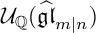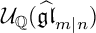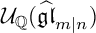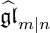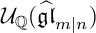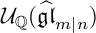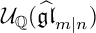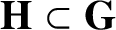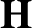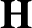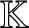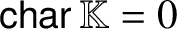Refine listing
Actions for selected content:
279 results in 20Gxx
Explicit calculations in an infinitesimal singular block of SLn
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 10 February 2022, pp. 19-52
-
- Article
- Export citation
BOHR COMPACTIFICATIONS OF GROUPS AND RINGS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 04 February 2022, pp. 1103-1137
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON ÉTALE REPRESENTATIONS FROM NILPOTENT ORBITS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 25 January 2022, pp. 113-125
- Print publication:
- August 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On multiplicative energy of subsets of varieties
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 13 January 2022, pp. 322-340
- Print publication:
- February 2023
-
- Article
- Export citation
On the multiplication of spherical functions of reductive spherical pairs of type A
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 09 December 2021, pp. 341-374
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the construction of tame supercuspidal representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 03 January 2022, pp. 2733-2746
- Print publication:
- December 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Corrigendum to ‘Endoscopy for Hecke categories, character sheaves and representations’
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 9 / 2021
- Published online by Cambridge University Press:
- 30 November 2021, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Tits–Weiss conjecture and the Kneser–Tits conjecture for
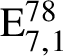 $\mathrm {E}^{78}_{7,1}$ and
$\mathrm {E}^{78}_{7,1}$ and 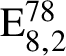 $\mathrm {E}^{78}_{8,2}$ (With an Appendix by R. M. Weiss)
$\mathrm {E}^{78}_{8,2}$ (With an Appendix by R. M. Weiss)
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 23 November 2021, e75
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Steenrod operators, the Coulomb branch and the Frobenius twist
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 04 November 2021, pp. 2494-2552
- Print publication:
- November 2021
-
- Article
- Export citation
A bimodule description of the Hecke category
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 30 September 2021, pp. 2133-2159
- Print publication:
- October 2021
-
- Article
- Export citation
The Allison–Faulkner construction of
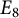 $E_8$
$E_8$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 10 September 2021, pp. 686-701
- Print publication:
- September 2022
-
- Article
- Export citation
A REALIZATION OF THE ENVELOPING SUPERALGEBRA
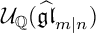 $ {\mathcal U}_{\mathbb Q}(\widehat {\mathfrak {gl}}_{m|n})$
$ {\mathcal U}_{\mathbb Q}(\widehat {\mathfrak {gl}}_{m|n})$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 247 / September 2022
- Published online by Cambridge University Press:
- 09 September 2021, pp. 516-551
- Print publication:
- September 2022
-
- Article
- Export citation
Cordial elements and dimensions of affine Deligne–Lusztig varieties
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 9 / 2021
- Published online by Cambridge University Press:
- 08 September 2021, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GENERALIZED GREEN FUNCTIONS AND UNIPOTENT CLASSES FOR FINITE REDUCTIVE GROUPS, III
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 247 / September 2022
- Published online by Cambridge University Press:
- 03 September 2021, pp. 552-573
- Print publication:
- September 2022
-
- Article
- Export citation
Annihilator varieties of distinguished modules of reductive Lie algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 26 July 2021, e52
-
- Article
-
- You have access
- Open access
- Export citation
Frobenius splitting of Schubert varieties of semi-infinite flag manifolds
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 9 / 2021
- Published online by Cambridge University Press:
- 13 July 2021, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE GENERIC FIBRE OF MODULI SPACES OF BOUNDED LOCAL G-SHTUKAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 12 July 2021, pp. 799-878
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Counting and equidistribution in quaternionic Heisenberg groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 1 / July 2022
- Published online by Cambridge University Press:
- 08 July 2021, pp. 67-104
- Print publication:
- July 2022
-
- Article
- Export citation
A group-theoretic generalization of the p-adic local monodromy theorem
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 29 June 2021, pp. 1450-1485
- Print publication:
- October 2022
-
- Article
- Export citation
Monoidal abelian envelopes
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 24 June 2021, pp. 1584-1609
- Print publication:
- July 2021
-
- Article
- Export citation