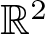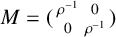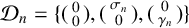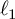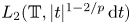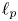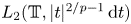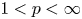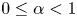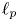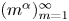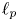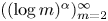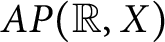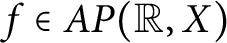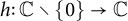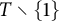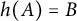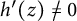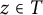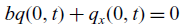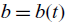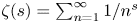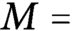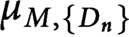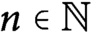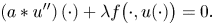Refine listing
Actions for selected content:
97 results in 42Axx
The Lp convergence of Fourier series on triangular domains
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 19 June 2023, pp. 453-474
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Logan’s problem for Jacobi transforms
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 24 April 2023, pp. 915-945
- Print publication:
- June 2024
-
- Article
- Export citation
Abstract almost periodicity for group actions on uniform topological spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 11 April 2023, pp. 798-829
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NONSPECTRAL PROBLEM FOR PLANAR MORAN–SIERPINSKI MEASURES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 11 January 2023, pp. 308-319
- Print publication:
- October 2023
-
- Article
- Export citation
Brownian bridge expansions for Lévy area approximations and particular values of the Riemann zeta function
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 03 November 2022, pp. 370-397
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Divergence of mock Fourier series for spectral measures
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 17 October 2022, pp. 1818-1832
- Print publication:
- December 2023
-
- Article
- Export citation
VARIANTS OF A MULTIPLIER THEOREM OF KISLYAKOV
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 01 September 2022, pp. 347-377
- Print publication:
- January 2024
-
- Article
- Export citation
Bounds for spectral projectors on tori
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 12 May 2022, e24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THREE-DIMENSIONAL ANALYTICAL SOLUTION OF THE ADVECTION-DIFFUSION EQUATION FOR AIR POLLUTION DISPERSION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 26 April 2022, pp. 40-53
-
- Article
- Export citation
Fourier coefficients of functions in power-weighted L2-spaces and conditionality constants of bases in Banach spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 30 March 2022, pp. 784-810
- Print publication:
- June 2023
-
- Article
- Export citation
A note on spaces of almost periodic functions with values in Banach spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 18 January 2022, pp. 953-962
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A generalized Davenport expansion
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 26 August 2021, pp. 711-715
-
- Article
- Export citation
Analytic order-isomorphisms of countable dense subsets of the unit circle
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 14 July 2021, pp. 653-664
- Print publication:
- September 2022
-
- Article
- Export citation
Linear evolution equations on the half-line with dynamic boundary conditions
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 33 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 03 May 2021, pp. 505-537
-
- Article
- Export citation
Fourier transforms related to ζ(s)
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 200-216
-
- Article
- Export citation
Spectrality of Moran Sierpinski-type measures on
 ${\mathbb R}^2$
${\mathbb R}^2$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 18 January 2021, pp. 1024-1040
- Print publication:
- December 2021
-
- Article
- Export citation
Dispersive fractalisation in linear and nonlinear Fermi–Pasta–Ulam–Tsingou lattices
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 12 January 2021, pp. 820-845
-
- Article
-
- You have access
- Open access
- Export citation
Existence and monotonicity of nonlocal boundary value problems: the one-dimensional case
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 23 December 2020, pp. 1-27
- Print publication:
- February 2022
-
- Article
- Export citation
Uniform convergence rate for Birkhoff means of certain uniquely ergodic toral maps
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 06 October 2020, pp. 3363-3388
- Print publication:
- November 2021
-
- Article
- Export citation
Approximation via Hausdorff operators
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 13 August 2020, pp. 512-529
- Print publication:
- September 2021
-
- Article
-
- You have access
- Open access
- Export citation