Refine listing
Actions for selected content:
97 results in 42Axx
Turán-Type Inequalities for Some Lommel Functions of the First Kind
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 29 October 2015, pp. 569-579
-
- Article
- Export citation
ON THE MINIMAL PROPERTY OF DE LA VALLÉE POUSSIN’S OPERATOR
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 08 October 2014, pp. 129-133
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
A VARIATION ON SELBERG’S APPROXIMATION PROBLEM
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 14 August 2014, pp. 213-235
- Print publication:
- January 2015
-
- Article
- Export citation
CHARACTERISATIONS OF HARDY GROWTH SPACES WITH DOUBLING WEIGHTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 12 May 2014, pp. 275-282
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
Probabilities of Competing Binomial Random Variables
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 49 / Issue 3 / September 2012
- Published online by Cambridge University Press:
- 04 February 2016, pp. 731-744
- Print publication:
- September 2012
-
- Article
-
- You have access
- Export citation
FOURIER ANALYSIS AND THE KINETIC THEORY OF GASES
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 16 December 2011, pp. 93-208
- Print publication:
- January 2012
-
- Article
- Export citation
On the completeness of sets of complex exponentials
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 14 / 2011
- Published online by Cambridge University Press:
- 01 June 2011, pp. 137-139
-
- Article
-
- You have access
- Export citation
WEIGHTED PSEUDO-ALMOST PERIODIC SOLUTIONS FOR SOME ABSTRACT DIFFERENTIAL EQUATIONS WITH UNIFORM CONTINUITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 13 October 2010, pp. 424-436
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
Exponential Squared Integrability of the Discrepancy Function in Two Dimensions
- Part of
-
- Journal:
- Mathematika / Volume 55 / Issue 1-2 / December 2009
- Published online by Cambridge University Press:
- 21 December 2009, pp. 1-27
- Print publication:
- December 2009
-
- Article
- Export citation
ORTHOGONAL FUNCTIONS AND ZERNIKE POLYNOMIALS—A RANDOM VARIABLE INTERPRETATION
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 50 / Issue 3 / January 2009
- Published online by Cambridge University Press:
- 03 November 2009, pp. 435-444
-
- Article
-
- You have access
- Export citation
On the Littlewood Problem Modulo a Prime
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 61 / Issue 1 / 01 February 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 141-164
- Print publication:
- 01 February 2009
-
- Article
-
- You have access
- Export citation
I0 SETS FOR COMPACT, CONNECTED GROUPS: INTERPOLATION WITH MEASURES THAT ARE NONNEGATIVE OR OF SMALL SUPPORT
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 199-215
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
Operator-valued multiplier theorems characterizing Hilbert spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 2 / October 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 175-184
- Print publication:
- October 2004
-
- Article
-
- You have access
- Export citation
Vector valued mean-periodic functions on groups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 3 / June 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 363-388
- Print publication:
- June 2002
-
- Article
-
- You have access
- Export citation
Analogies and correspondences between variograms and covariance functions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 33 / Issue 3 / September 2001
- Published online by Cambridge University Press:
- 01 July 2016, pp. 617-630
- Print publication:
- September 2001
-
- Article
- Export citation
Lacunarity on nonabelian groups and summing operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 71 / Issue 1 / August 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 71-79
- Print publication:
- August 2001
-
- Article
-
- You have access
- Export citation
Norm inequalities relating one-sided singular integrals and the one-sided maximal function
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 3 / December 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 403-414
- Print publication:
- December 2000
-
- Article
-
- You have access
- Export citation
Power-law correlations, related models for long-range dependence and their simulation
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 37 / Issue 4 / December 2000
- Published online by Cambridge University Press:
- 14 July 2016, pp. 1104-1109
- Print publication:
- December 2000
-
- Article
- Export citation
A family of strongly singular operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 67 / Issue 1 / August 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 58-84
- Print publication:
- August 1999
-
- Article
-
- You have access
- Export citation
Strong summability for the Marcinkiewicz means in the integral metric and related questions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 3 / December 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 303-312
- Print publication:
- December 1998
-
- Article
-
- You have access
- Export citation
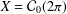
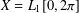
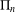

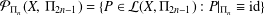
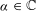
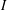
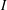

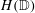
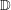
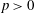
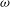
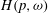
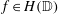
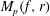
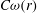
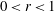
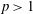
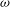
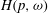
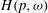
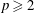
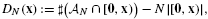
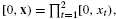 and |[
and |[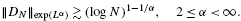
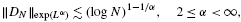
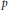
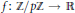
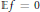
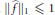
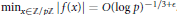
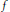
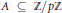
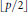
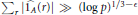
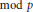
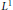

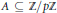
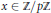
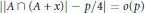
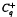 condition, then the
condition, then the 