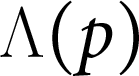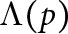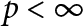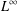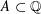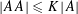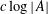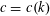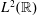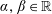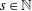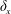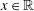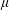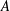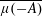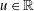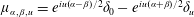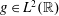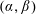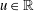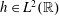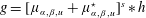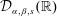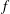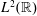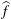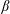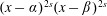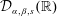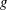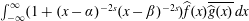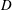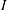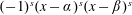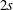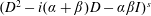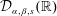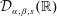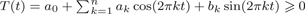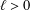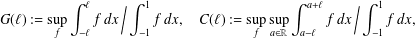Refine listing
Actions for selected content:
97 results in 42Axx
NOTE ON FOURIER–STIELTJES COEFFICIENTS OF COIN-TOSSING MEASURES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 20 April 2020, pp. 479-489
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
A Non-abelian, Non-Sidon, Completely Bounded
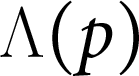 $\Lambda (p)$ Set
$\Lambda (p)$ Set
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 26 February 2020, pp. 1-7
- Print publication:
- March 2021
-
- Article
- Export citation
ALGEBRAIC STRUCTURE OF THE RANGE OF A TRIGONOMETRIC POLYNOMIAL
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 251-260
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
Positive Definiteness on Products of Compact Two-point Homogeneous Spaces and Locally Compact Abelian Groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 29 October 2019, pp. 705-715
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
ON LITTLEWOOD’S PROOF OF THE PRIME NUMBER THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 15 August 2019, pp. 226-232
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
A comparison principle for convolution measures with applications
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 2 / September 2020
- Published online by Cambridge University Press:
- 28 June 2019, pp. 307-322
- Print publication:
- September 2020
-
- Article
- Export citation
Higher Summability and Discrete Weighted Muckenhoupt and Gehring Type Inequalities
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 4 / November 2019
- Published online by Cambridge University Press:
- 11 March 2019, pp. 949-973
-
- Article
- Export citation
RECOVERY OF THE TEMPERATURE DISTRIBUTION IN A MULTILAYER FRACTIONAL DIFFUSION EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 20 February 2019, pp. 344-352
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
On the Fourier Transformability of Strongly Almost Periodic Measures
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 29 January 2019, pp. 900-927
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Uniform Convergence of Trigonometric Series with General Monotone Coefficients
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 1445-1463
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
ON ITERATED PRODUCT SETS WITH SHIFTS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 4 / 2019
- Published online by Cambridge University Press:
- 21 May 2019, pp. 831-850
- Print publication:
- 2019
-
- Article
- Export citation
Sidon Sets are Proportionally Sidon with Small Sidon Constants
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 11 December 2018, pp. 798-809
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Vanishing Fourier Transforms and Generalized Differences in
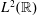 $L^{2}(\mathbb{R})$
$L^{2}(\mathbb{R})$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 16 October 2018, pp. 393-404
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
FOURIER-TYPE TRANSFORMS ON REARRANGEMENT-INVARIANT QUASI-BANACH FUNCTION SPACES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 20 June 2018, pp. 231-248
-
- Article
-
- You have access
- Export citation
The Point Value Maximization Problem for Positive Definite Functions Supported in a Given Subset of a Locally Compact Group
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 24 January 2018, pp. 179-200
-
- Article
- Export citation
ON MULTIPLIERS BETWEEN SOME SPACES OF HOLOMORPHIC FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 29 March 2017, pp. 146-153
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
ON INTEGRAL ESTIMATES OF NONNEGATIVE POSITIVE DEFINITE FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 117-125
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
THE CONNECTION BETWEEN PSEUDO ALMOST PERIODIC FUNCTIONS DEFINED ON TIME SCALES AND ON THE REAL LINE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 22 February 2017, pp. 482-494
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
An almost-periodic solution of Hasegawa–Wakatani equations with vanishing resistivity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 5 / October 2016
- Published online by Cambridge University Press:
- 23 June 2016, pp. 983-1003
- Print publication:
- October 2016
-
- Article
- Export citation
Multiple Spectra of Bernoulli Convolutions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 10 May 2016, pp. 187-202
-
- Article
- Export citation