Refine listing
Actions for selected content:
97 results in 42Axx
An extension of the Fejér-Jackson inequality
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 62 / Issue 1 / February 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-12
- Print publication:
- February 1997
-
- Article
-
- You have access
- Export citation
On the L1-convergence of Fourier transforms
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 3 / June 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 405-420
- Print publication:
- June 1996
-
- Article
-
- You have access
- Export citation
Linear independence of translations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 59 / Issue 1 / August 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 131-133
- Print publication:
- August 1995
-
- Article
-
- You have access
- Export citation
The class L(log L)α and some lacunary sets
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 3 / June 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 387-403
- Print publication:
- June 1995
-
- Article
-
- You have access
- Export citation
Inequalities and representation formulas for functions of exponential type
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 1 / February 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 15-26
- Print publication:
- February 1995
-
- Article
-
- You have access
- Export citation
The abscissa of convergence of the Laplace transform
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 2 / June 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 353-362
- Print publication:
- June 1992
-
- Article
- Export citation
Pointwise estimates for an interpolation process of S. N. Bernstein
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 51 / Issue 2 / October 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 284-299
- Print publication:
- October 1991
-
- Article
-
- You have access
- Export citation
On Grasia's criterion for uniform convergence of Fourier series
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 51 / Issue 2 / October 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 305-323
- Print publication:
- October 1991
-
- Article
-
- You have access
- Export citation
Some trigonometric extremal problems and duality
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 3 / June 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 384-390
- Print publication:
- June 1991
-
- Article
-
- You have access
- Export citation
Almost everywhere convergence of lacunary trigonometric series with respect to Riesz products
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 48 / Issue 3 / June 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 376-383
- Print publication:
- June 1990
-
- Article
-
- You have access
- Export citation
Fourier series with small gaps
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 46 / Issue 2 / April 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 212-219
- Print publication:
- April 1989
-
- Article
-
- You have access
- Export citation
Ergodic measures for the irrational rotation on the circle
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 45 / Issue 1 / August 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 133-141
- Print publication:
- August 1988
-
- Article
-
- You have access
- Export citation
On the Integral Modulus of Continuity of Fourier Series
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 44 / Issue 2 / April 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 151-158
- Print publication:
- April 1988
-
- Article
-
- You have access
- Export citation
Pointwise Convergence of Trigonometric Series
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 43 / Issue 3 / December 1987
- Published online by Cambridge University Press:
- 09 April 2009, pp. 291-300
- Print publication:
- December 1987
-
- Article
-
- You have access
- Export citation
L1-convergence of Fourier series
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 41 / Issue 3 / December 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 376-390
- Print publication:
- December 1986
-
- Article
-
- You have access
- Export citation
Some inequalities for trigonometric polynomials
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 2 / October 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 216-226
- Print publication:
- October 1985
-
- Article
-
- You have access
- Export citation
A generalized Fourier transformation for L1(G)-Modules
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 36 / Issue 3 / June 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 365-377
- Print publication:
- June 1984
-
- Article
-
- You have access
- Export citation
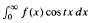 and
and 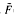 (
(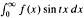 where
where 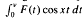 and
and 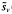
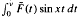 , the modified partial integrals
, the modified partial integrals 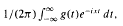 , where
, where 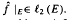 . In this paper we investigate similar results for the classes
. In this paper we investigate similar results for the classes 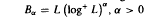 on an arbitrary infinite compact abelian group
on an arbitrary infinite compact abelian group 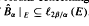 . We also prove partial results on the distinctness of the
. We also prove partial results on the distinctness of the 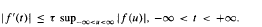 . Moreover we obtain a new representation formula for entire functions of exponential type.
. Moreover we obtain a new representation formula for entire functions of exponential type.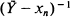 where
where 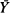 is the mean of the sample values overshooting
is the mean of the sample values overshooting 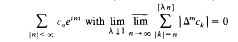 for some nonnegative integer
for some nonnegative integer 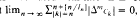 , where {
, where {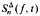 and establish its
and establish its 