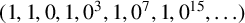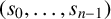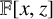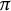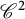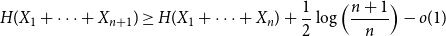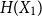Refine listing
Actions for selected content:
89 results in 94Axx
Quantization dimensions of negative order
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 11 November 2025, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-parametric estimation of the generalized past entropy function under α-mixing sample
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences , First View
- Published online by Cambridge University Press:
- 05 November 2025, pp. 1-16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Introducing and applying varinaccuracy: a measure for doubly truncated random variables in reliability analysis
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences , First View
- Published online by Cambridge University Press:
- 05 September 2025, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Relative entropy bounds for sampling with and without replacement
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 28 July 2025, pp. 1578-1593
- Print publication:
- December 2025
-
- Article
- Export citation
Sharp estimates for Gowers norms on discrete cubes
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 16 June 2025, pp. 1-27
-
- Article
- Export citation
Extropy-based dynamic cumulative residual inaccuracy measure: properties and applications
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 39 / Issue 4 / October 2025
- Published online by Cambridge University Press:
- 26 February 2025, pp. 461-485
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Some generalized information and divergence generating functions: properties, estimation, validation, and applications
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 39 / Issue 3 / July 2025
- Published online by Cambridge University Press:
- 25 February 2025, pp. 397-430
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE BINARY SEQUENCE
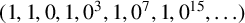 $(1,1,0,1,0^3,1,0^7,1,0^{15},\ldots )$
$(1,1,0,1,0^3,1,0^7,1,0^{15},\ldots )$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 23 October 2024, pp. 260-271
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A mathematical theory of super-resolution and two-point resolution
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 21 October 2024, e83
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON A CONJECTURE REGARDING THE SYMMETRIC DIFFERENCE OF CERTAIN SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 10 October 2024, pp. 397-404
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal experimental design: Formulations and computations
- Part of
-
- Journal:
- Acta Numerica / Volume 33 / July 2024
- Published online by Cambridge University Press:
- 04 September 2024, pp. 715-840
-
- Article
-
- You have access
- Open access
- Export citation
Quantile-based information generating functions and their properties and uses
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 4 / October 2024
- Published online by Cambridge University Press:
- 22 May 2024, pp. 733-751
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Phase retrieval on circles and lines
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 10 May 2024, pp. 927-935
- Print publication:
- December 2024
-
- Article
- Export citation
Convergence rate of entropy-regularized multi-marginal optimal transport costs
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 15 March 2024, pp. 1072-1092
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Ziv–Merhav theorem beyond Markovianity I
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 07 March 2024, pp. 891-915
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unified bounds for the independence number of graphs
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 11 December 2023, pp. 97-117
- Print publication:
- February 2025
-
- Article
- Export citation
t-Design Curves and Mobile Sampling on the Sphere
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 23 November 2023, e105
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Approximate discrete entropy monotonicity for log-concave sums
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 13 November 2023, pp. 196-209
-
- Article
- Export citation
Markov capacity for factor codes with an unambiguous symbol
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 07 November 2023, pp. 2199-2228
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The unified extropy and its versions in classical and Dempster–Shafer theories
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 23 October 2023, pp. 685-696
- Print publication:
- June 2024
-
- Article
- Export citation