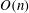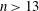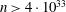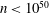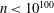Refine listing
Actions for selected content:
89 results in 94Axx
THE RESTRICTED ISOMETRY PROPERTY FOR SIGNAL RECOVERY WITH COHERENT TIGHT FRAMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 19 August 2015, pp. 496-507
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
Capacity and Error Exponents of Stationary Point Processes under Random Additive Displacements
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 04 January 2016, pp. 1-26
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
Lumpings of Markov Chains, Entropy Rate Preservation, and Higher-Order Lumpability
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 51 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 30 January 2018, pp. 1114-1132
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
The discrete logarithm problem for exponents of bounded height
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 148-156
-
- Article
-
- You have access
- Export citation
Hyper-and-elliptic-curve cryptography
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue A / 2014
- Published online by Cambridge University Press:
- 01 August 2014, pp. 181-202
-
- Article
-
- You have access
- Export citation
AN EFFICIENT METHOD FOR IMPROVING THE COMPUTATIONAL PERFORMANCE OF THE CUBIC LUCAS CRYPTOSYSTEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 10 April 2014, pp. 160-171
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
Wieferich pairs and Barker sequences, II
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 24-32
-
- Article
-
- You have access
- Export citation
Local Digital Estimators of Intrinsic Volumes for Boolean Models and in the Design-Based Setting
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 1 / March 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 35-58
- Print publication:
- March 2014
-
- Article
-
- You have access
- Export citation
On the use of expansion series for stream ciphers
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 September 2012, pp. 326-340
-
- Article
-
- You have access
- Export citation
COUNTING FIXED POINTS, TWO-CYCLES, AND COLLISIONS OF THE DISCRETE EXPONENTIAL FUNCTION USING p-ADIC METHODS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 22 November 2012, pp. 163-178
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
BOUNDS IN TERMS OF GÂTEAUX DERIVATIVES FOR THE WEIGHTED f-GINI MEAN DIFFERENCE IN LINEAR SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 83 / Issue 3 / June 2011
- Published online by Cambridge University Press:
- 01 April 2011, pp. 420-434
- Print publication:
- June 2011
-
- Article
-
- You have access
- Export citation
ENDPOINT ESTIMATES FOR COMMUTATORS OF RIESZ TRANSFORMS ASSOCIATED WITH SCHRÖDINGER OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 16 August 2010, pp. 367-389
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
SAMPLING AND BIRKHOFF REGULAR PROBLEMS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 87 / Issue 3 / December 2009
- Published online by Cambridge University Press:
- 15 December 2009, pp. 289-310
- Print publication:
- December 2009
-
- Article
-
- You have access
- Export citation
SECURE AND PRIVATE FINGERPRINT-BASED AUTHENTICATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 2 / October 2009
- Published online by Cambridge University Press:
- 04 September 2009, pp. 347-349
- Print publication:
- October 2009
-
- Article
-
- You have access
- Export citation
CODES ASSOCIATED WITH Sp(4,q) AND EVEN-POWER MOMENTS OF KLOOSTERMAN SUMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 3 / June 2009
- Published online by Cambridge University Press:
- 17 April 2009, pp. 427-435
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
Large deviations for eigenvalues of sample covariance matrices, with applications to mobile communication systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 40 / Issue 4 / December 2008
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1048-1071
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
A Central Limit Theorem for Non-Overlapping Return Times
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 43 / Issue 1 / March 2006
- Published online by Cambridge University Press:
- 14 July 2016, pp. 32-47
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
Power spectra of random spike fields and related processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 37 / Issue 4 / December 2005
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1116-1146
- Print publication:
- December 2005
-
- Article
-
- You have access
- Export citation
Minimum dynamic discrimination information models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 42 / Issue 3 / September 2005
- Published online by Cambridge University Press:
- 14 July 2016, pp. 643-660
- Print publication:
- September 2005
-
- Article
-
- You have access
- Export citation
Improving the performance of third-generation wireless communication systems
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 36 / Issue 4 / December 2004
- Published online by Cambridge University Press:
- 01 July 2016, pp. 1046-1084
- Print publication:
- December 2004
-
- Article
- Export citation