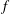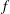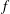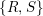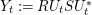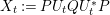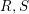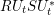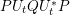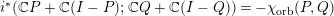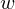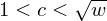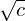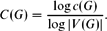Refine listing
Actions for selected content:
89 results in 94Axx
CALDERÓN’S INVERSE PROBLEM WITH A FINITE NUMBER OF MEASUREMENTS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 08 October 2019, e35
-
- Article
-
- You have access
- Open access
- Export citation
Orlicz Addition for Measures and an Optimization Problem for the
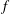 $f$-divergence
$f$-divergence
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 16 July 2019, pp. 455-479
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
CONVEXITY OF PARAMETER EXTENSIONS OF SOME RELATIVE OPERATOR ENTROPIES WITH A PERSPECTIVE APPROACH
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 06 June 2019, pp. 737-744
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
SYMMETRIC ITINERARY SETS: ALGORITHMS AND NONLINEAR EXAMPLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 20 March 2019, pp. 109-118
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
CHECKERBOARD COPULAS OF MAXIMUM ENTROPY WITH PRESCRIBED MIXED MOMENTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 26 November 2018, pp. 302-318
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
PROPERTIES FOR GENERALIZED CUMULATIVE PAST MEASURES OF INFORMATION
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 34 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 29 October 2018, pp. 92-111
-
- Article
- Export citation
LIBERATION, FREE MUTUAL INFORMATION AND ORBITAL FREE ENTROPY
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 239 / September 2020
- Published online by Cambridge University Press:
- 14 September 2018, pp. 205-231
- Print publication:
- September 2020
-
- Article
-
- You have access
- HTML
- Export citation
Connections of Gini, Fisher, and Shannon by Bayes risk under proportional hazards
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 4 / December 2017
- Published online by Cambridge University Press:
- 30 November 2017, pp. 1027-1050
- Print publication:
- December 2017
-
- Article
- Export citation
Some properties of the cumulative residual entropy of coherent and mixed systems
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 54 / Issue 2 / June 2017
- Published online by Cambridge University Press:
- 22 June 2017, pp. 379-393
- Print publication:
- June 2017
-
- Article
- Export citation
IMAGE INPAINTING FROM PARTIAL NOISY DATA BY DIRECTIONAL COMPLEX TIGHT FRAMELETS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 3-4 / April 2017
- Published online by Cambridge University Press:
- 26 May 2017, pp. 247-255
-
- Article
-
- You have access
- Export citation
BREAKING THE COHERENCE BARRIER: A NEW THEORY FOR COMPRESSED SENSING
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 15 February 2017, e4
-
- Article
-
- You have access
- Open access
- Export citation
Fast Linearized Augmented Lagrangian Method for Euler's Elastica Model
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 20 February 2017, pp. 98-115
- Print publication:
- February 2017
-
- Article
- Export citation
Total Variation Based Parameter-Free Model for Impulse Noise Removal
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 20 February 2017, pp. 186-204
- Print publication:
- February 2017
-
- Article
- Export citation
The Boolean model in the Shannon regime: three thresholds and related asymptotics
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 4 / December 2016
- Published online by Cambridge University Press:
- 09 December 2016, pp. 1001-1018
- Print publication:
- December 2016
-
- Article
- Export citation
Reduced memory meet-in-the-middle attackagainst the NTRU private key
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 43-57
-
- Article
-
- You have access
- Export citation
Algorithms for the approximate common divisor problem
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 58-72
-
- Article
-
- You have access
- Export citation
An Anisotropic Convection-Diffusion Model Using Tailored Finite Point Method for Image Denoising and Compression
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 17 May 2016, pp. 1357-1374
- Print publication:
- May 2016
-
- Article
- Export citation
On the Normalized Shannon Capacity of a Union
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 5 / September 2016
- Published online by Cambridge University Press:
- 03 March 2016, pp. 766-767
-
- Article
- Export citation
On dynamic mutual information for bivariate lifetimes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 47 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 21 March 2016, pp. 1157-1174
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
Extension of the past lifetime and its connection to the cumulative entropy
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 30 March 2016, pp. 1156-1174
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation