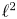 -betti number and groups acting on trees
-betti number and groups acting on trees
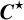 ${\mathit{C}}^{\star }$
-ALGEBRAS OF 2-RANK GRAPHS ASSOCIATED TO COMPLETE BIPARTITE GRAPHS
${\mathit{C}}^{\star }$
-ALGEBRAS OF 2-RANK GRAPHS ASSOCIATED TO COMPLETE BIPARTITE GRAPHS