Refine listing
Actions for selected content:
163 results in 57Rxx
ON OVERTWISTED CONTACT SURGERIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 03 May 2018, pp. 144-148
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
HILBERT STRATIFOLDS AND A QUILLEN TYPE GEOMETRIC DESCRIPTION OF COHOMOLOGY FOR HILBERT MANIFOLDS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 27 February 2018, e4
-
- Article
-
- You have access
- Open access
- Export citation
Non-Negative Curvature, Elliptic Genus and Unbounded Pontryagin Numbers
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 26 February 2018, pp. 449-456
-
- Article
- Export citation
Nearby Lagrangian fibers and Whitney sphere links
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 4 / April 2018
- Published online by Cambridge University Press:
- 20 February 2018, pp. 685-718
- Print publication:
- April 2018
-
- Article
- Export citation
How do autodiffeomorphisms act on embeddings?
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 4 / August 2018
- Published online by Cambridge University Press:
- 28 December 2017, pp. 835-848
- Print publication:
- August 2018
-
- Article
- Export citation
ON POWERS OF HALF-TWISTS IN M(0, 2n)
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 30 October 2017, pp. 333-338
- Print publication:
- May 2018
-
- Article
-
- You have access
- Export citation
Strong cohomological rigidity of toric varieties
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 5 / October 2017
- Published online by Cambridge University Press:
- 25 September 2017, pp. 971-992
- Print publication:
- October 2017
-
- Article
- Export citation
Closure of singular foliations: the proof ofMolino’s conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 12 / December 2017
- Published online by Cambridge University Press:
- 13 September 2017, pp. 2577-2590
- Print publication:
- December 2017
-
- Article
- Export citation
INVOLUTIVE HEEGAARD FLOER HOMOLOGY AND PLUMBED THREE-MANIFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 6 / November 2019
- Published online by Cambridge University Press:
- 04 September 2017, pp. 1115-1155
- Print publication:
- November 2019
-
- Article
- Export citation
Bifurcation values of families of real curves
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 6 / December 2017
- Published online by Cambridge University Press:
- 31 May 2017, pp. 1233-1242
- Print publication:
- December 2017
-
- Article
- Export citation
ORBIFOLD POINTS ON PRYM–TEICHMÜLLER CURVES IN GENUS
 $4$
$4$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 4 / July 2019
- Published online by Cambridge University Press:
- 22 May 2017, pp. 673-706
- Print publication:
- July 2019
-
- Article
- Export citation
THE FOLIATED LEFSCHETZ HYPERPLANE THEOREM
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 231 / September 2018
- Published online by Cambridge University Press:
- 10 May 2017, pp. 115-127
- Print publication:
- September 2018
-
- Article
-
- You have access
- HTML
- Export citation
Tautological rings for high-dimensional manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 4 / April 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 851-866
- Print publication:
- April 2017
-
- Article
- Export citation
Bifurcation sets of families of reflections on surfaces in ℝ3
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 14 February 2017, pp. 337-352
- Print publication:
- April 2017
-
- Article
- Export citation
On the contact mapping class group ofLegendrian circle bundles
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 2 / February 2017
- Published online by Cambridge University Press:
- 01 February 2017, pp. 294-312
- Print publication:
- February 2017
-
- Article
- Export citation
Normal developable surfaces of surfaces along curves
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 06 January 2017, pp. 177-203
- Print publication:
- February 2017
-
- Article
- Export citation
NONSURJECTIVE SATELLITE OPERATORS AND PIECEWISE-LINEAR CONCORDANCE
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 23 December 2016, e34
-
- Article
-
- You have access
- Open access
- Export citation
EMBEDDINGS, NORMAL INVARIANTS AND FUNCTOR CALCULUS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 225 / March 2017
- Published online by Cambridge University Press:
- 19 August 2016, pp. 152-184
- Print publication:
- March 2017
-
- Article
-
- You have access
- HTML
- Export citation
ORBISPACES, CONFIGURATIONS AND QUASI-FIBRATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 16 August 2016, p. 342
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
Maximal Thurston–Bennequin number and reducible Legendrian surgery
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 9 / September 2016
- Published online by Cambridge University Press:
- 30 June 2016, pp. 1899-1914
- Print publication:
- September 2016
-
- Article
- Export citation
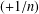
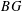
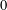
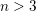
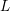
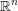
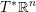
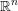
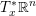
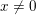
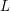
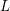

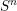
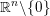
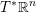
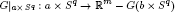
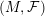
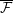
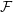

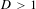
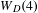
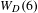
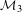
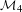
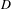
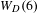

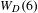

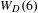
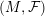
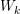
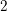
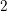
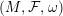
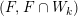
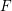
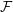
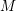
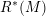
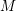
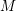
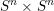

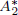 points’, which are not detected by the flat geometry of the surface. These
points’, which are not detected by the flat geometry of the surface. These