Refine listing
Actions for selected content:
163 results in 57Rxx
LOOP GROUPS, STRING CLASSES AND EQUIVARIANT COHOMOLOGY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 22 March 2011, pp. 109-127
- Print publication:
- February 2011
-
- Article
-
- You have access
- Export citation
Dehn surgeries on some classical links
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 19 January 2011, pp. 33-45
-
- Article
-
- You have access
- Export citation
The Lalonde–McDuff Conjecture and the fundamental group
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 28 October 2010, pp. 125-129
-
- Article
-
- You have access
- Export citation
Contact surgeries and the transverse invariant in knot Floer homology
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 9 / Issue 3 / July 2010
- Published online by Cambridge University Press:
- 11 May 2010, pp. 601-632
- Print publication:
- July 2010
-
- Article
- Export citation
The diffeotopy group of S1×S2 via contact topology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 146 / Issue 4 / July 2010
- Published online by Cambridge University Press:
- 18 March 2010, pp. 1096-1112
- Print publication:
- July 2010
-
- Article
-
- You have access
- Export citation
Spectral numbers in Floer theories
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 6 / November 2008
- Published online by Cambridge University Press:
- 01 November 2008, pp. 1581-1592
- Print publication:
- November 2008
-
- Article
-
- You have access
- Export citation
Symplectomorphism groups and embeddings of balls into rational ruled 4-manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 3 / May 2008
- Published online by Cambridge University Press:
- 01 May 2008, pp. 787-810
- Print publication:
- May 2008
-
- Article
-
- You have access
- Export citation
TRANSVERSAL HARMONIC THEORY FOR TRANSVERSALLY SYMPLECTIC FLOWS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 233-245
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation
Maximal symplectic packings in
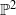
- Part of
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 6 / November 2007
- Published online by Cambridge University Press:
- 01 November 2007, pp. 1558-1575
- Print publication:
- November 2007
-
- Article
-
- You have access
- Export citation
A note on the theta characteristics of a compact Riemann surface
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 76 / Issue 3 / June 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 415-424
- Print publication:
- June 2004
-
- Article
-
- You have access
- Export citation
Finite group actions on 4-manifolds
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 3 / June 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 287-296
- Print publication:
- June 1999
-
- Article
-
- You have access
- Export citation
Non-embeddings of the real flag manifolds RF (1, 1, n – 2)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 1 / February 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 51-55
- Print publication:
- February 1999
-
- Article
-
- You have access
- Export citation
The Vanishing problem of the string class with degree 3
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 65 / Issue 1 / August 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 129-142
- Print publication:
- August 1998
-
- Article
-
- You have access
- Export citation
Compressible ends of leaves in foliated 3-manifolds
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 63 / Issue 2 / October 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 208-217
- Print publication:
- October 1997
-
- Article
-
- You have access
- Export citation
On the vanishing problem of string classes
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 61 / Issue 2 / October 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 258-266
- Print publication:
- October 1996
-
- Article
-
- You have access
- Export citation
Holonomy and basic cohomology of foliations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 3 / June 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 287-300
- Print publication:
- June 1996
-
- Article
-
- You have access
- Export citation
The least number of coincidence points on surfaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 1 / February 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 27-38
- Print publication:
- February 1995
-
- Article
-
- You have access
- Export citation
Detecting exotic structures via the Pontrjagin-Thom construction
- Part of
-
- Journal:
- Mathematika / Volume 41 / Issue 1 / June 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 145-148
- Print publication:
- June 1994
-
- Article
- Export citation
Almost identical imitations of (3,1)-dimensional manifold pairs and the manifold mutation
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 55 / Issue 1 / August 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 100-115
- Print publication:
- August 1993
-
- Article
-
- You have access
- Export citation
Symplectic complex bundles over real algebraic four-folds
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 3 / December 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 430-437
- Print publication:
- December 1989
-
- Article
-
- You have access
- Export citation
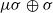 normalized so that
normalized so that 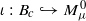 of the standard ball of capacity
of the standard ball of capacity 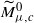 . In this paper, we study the homotopy type of the symplectomorphism group
. In this paper, we study the homotopy type of the symplectomorphism group 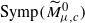 and that of the space
and that of the space 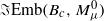 of unparametrized symplectic embeddings of
of unparametrized symplectic embeddings of 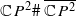 obtained by blowing down
obtained by blowing down 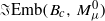 is homotopy equivalent to
is homotopy equivalent to 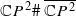 . By contrast, we show that the embedding spaces
. By contrast, we show that the embedding spaces 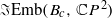 and
and 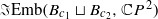 , if non-empty, are always homotopy equivalent to the spaces of ordered configurations
, if non-empty, are always homotopy equivalent to the spaces of ordered configurations 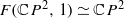 and
and 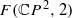 . Our method relies on the theory of pseudo-holomorphic curves in 4 -manifolds, on the computation of Gromov invariants in rational 4 -manifolds, and on the inflation technique of Lalonde and McDuff.
. Our method relies on the theory of pseudo-holomorphic curves in 4 -manifolds, on the computation of Gromov invariants in rational 4 -manifolds, and on the inflation technique of Lalonde and McDuff.
 (
(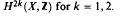 .
.