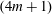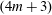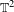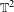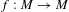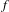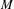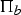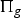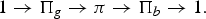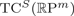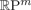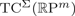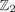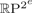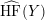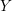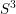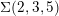Refine listing
Actions for selected content:
163 results in 57Rxx
A characterization of 3D steady Euler flows using commuting zero-flux homologies
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 18 March 2020, pp. 2166-2181
- Print publication:
- July 2021
-
- Article
-
- You have access
- Open access
- Export citation
On Open Book Embedding of Contact Manifolds in the Standard Contact Sphere
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 18 December 2019, pp. 755-770
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
Arithmeticity of the monodromy of some Kodaira fibrations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 26 November 2019, pp. 114-157
- Print publication:
- January 2020
-
- Article
- Export citation
Anosov diffeomorphisms of products I. Negative curvature and rational homology spheres
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 18 October 2019, pp. 553-569
- Print publication:
- February 2021
-
- Article
- Export citation
Endperiodic automorphisms of surfaces and foliations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 07 October 2019, pp. 66-212
- Print publication:
- January 2021
-
- Article
- Export citation
Partially hyperbolic surface endomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 03 September 2019, pp. 272-282
- Print publication:
- January 2021
-
- Article
- Export citation
Open manifolds with non-homeomorphic positively curved souls
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 2 / September 2020
- Published online by Cambridge University Press:
- 11 July 2019, pp. 357-376
- Print publication:
- September 2020
-
- Article
- Export citation
Codimension one compact center foliations are uniformly compact
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 9 / September 2020
- Published online by Cambridge University Press:
- 13 March 2019, pp. 2349-2367
- Print publication:
- September 2020
-
- Article
- Export citation
EXPLICIT cocycle formulas on finite abelian groups with applications to braided linear Gr-categories and Dijkgraaf–Witten invariants
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 4 / August 2020
- Published online by Cambridge University Press:
- 13 March 2019, pp. 1937-1964
- Print publication:
- August 2020
-
- Article
- Export citation
A Note on the Fundamental Group of Kodaira Fibrations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 30 January 2019, pp. 739-746
-
- Article
- Export citation
Evolutes and focal surfaces of framed immersions in the Euclidean space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 497-516
- Print publication:
- February 2020
-
- Article
- Export citation
Classification of knotted tori
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 22 January 2019, pp. 549-567
- Print publication:
- April 2020
-
- Article
- Export citation
An n-dimensional Klein bottle
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1207-1221
- Print publication:
- October 2019
-
- Article
- Export citation
Some results on extension of maps and applications
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 16 January 2019, pp. 1465-1472
- Print publication:
- December 2019
-
- Article
- Export citation
The Mod Two Cohomology of the Moduli Space of Rank Two Stable Bundles on a Surface and Skew Schur Polynomials
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 683-715
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
CONFIGURATION CATEGORIES AND HOMOTOPY AUTOMORPHISMS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 1 / January 2020
- Published online by Cambridge University Press:
- 19 November 2018, pp. 13-41
- Print publication:
- January 2020
-
- Article
-
- You have access
- Export citation
Unique ergodicity of the horocycle flow on Riemannnian foliations
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 13 November 2018, pp. 1459-1479
- Print publication:
- June 2020
-
- Article
- Export citation
Symmetric Bi-Skew Maps and Symmetrized Motion Planning in Projective Spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 06 August 2018, pp. 1087-1100
-
- Article
- Export citation
FOCAL SURFACES OF WAVE FRONTS IN THE EUCLIDEAN 3-SPACE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 13 July 2018, pp. 425-440
- Print publication:
- May 2019
-
- Article
-
- You have access
- Export citation
Bordered Floer homology and existence of incompressible tori in homology spheres
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 6 / June 2018
- Published online by Cambridge University Press:
- 18 May 2018, pp. 1222-1268
- Print publication:
- June 2018
-
- Article
- Export citation