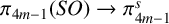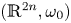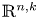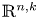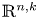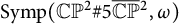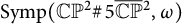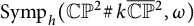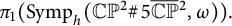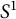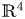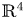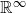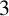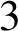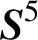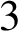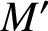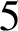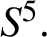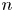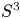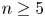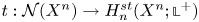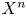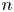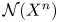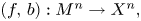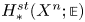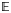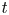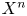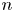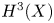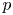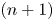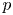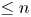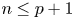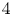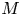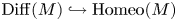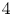Refine listing
Actions for selected content:
163 results in 57Rxx
Thurston’s fragmentation and c-principles
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 25 April 2023, e34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bordered Floer homology and contact structures
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 14 April 2023, e30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Enough vector bundles on orbispaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 28 November 2022, pp. 2046-2081
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SIMPLY CONNECTED MANIFOLDS WITH LARGE HOMOTOPY STABLE CLASSES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 115 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 26 September 2022, pp. 172-203
- Print publication:
- October 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Coisotropic Ekeland–Hofer capacities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 05 September 2022, pp. 1564-1608
- Print publication:
- October 2023
-
- Article
- Export citation
Leafwise quasigeodesic foliations in dimension three and the funnel property
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 8 / August 2023
- Published online by Cambridge University Press:
- 31 August 2022, pp. 2624-2650
- Print publication:
- August 2023
-
- Article
- Export citation
The symplectic isotopy problem for rational cuspidal curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 7 / July 2022
- Published online by Cambridge University Press:
- 16 September 2022, pp. 1595-1682
- Print publication:
- July 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Loops in the fundamental group of
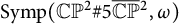 ${\mbox{Symp}} ({\mathbb C}{\mathbb P}^2\# \mbox{5}\overline { \mathbb C\mathbb P}\,\!^2,\omega )$ which are not represented by circle actions
${\mbox{Symp}} ({\mathbb C}{\mathbb P}^2\# \mbox{5}\overline { \mathbb C\mathbb P}\,\!^2,\omega )$ which are not represented by circle actions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 30 June 2022, pp. 1226-1271
- Print publication:
- August 2023
-
- Article
- Export citation
Equivariant cobordisms between freely periodic knots
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 22 June 2022, pp. 450-457
- Print publication:
- June 2023
-
- Article
- Export citation
Singularities of 3-parameter line congruences in $\mathbb {R}^{4}$
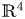
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 21 June 2022, pp. 1045-1070
- Print publication:
- June 2023
-
- Article
- Export citation
Decoupling Decorations on Moduli Spaces of Manifolds
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 10 May 2022, pp. 163-198
- Print publication:
- January 2023
-
- Article
- Export citation
CONTACT SURGERY GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 25 April 2022, pp. 146-157
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON OPEN BOOK EMBEDDINGS OF
 $3$-MANIFOLDS IN
$3$-MANIFOLDS IN 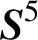 $\boldsymbol {S}^5$
$\boldsymbol {S}^5$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 04 October 2021, pp. 499-506
- Print publication:
- June 2022
-
- Article
- Export citation
Embedding spheres in knot traces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 20 October 2021, pp. 2242-2279
- Print publication:
- October 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generalized manifolds, normal invariants, and 𝕃-homology
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 16 June 2021, pp. 574-589
-
- Article
- Export citation
Studies of distance one surgeries on the lens space L(p, 1)
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 07 June 2021, pp. 267-301
- Print publication:
- March 2022
-
- Article
- Export citation
The homotopy classification of four-dimensional toric orbifolds
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 25 May 2021, pp. 626-648
- Print publication:
- June 2022
-
- Article
- Export citation
Galois symmetries of knot spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 29 April 2021, pp. 997-1021
- Print publication:
- May 2021
-
- Article
- Export citation
Rigidity of the mod 2 families Seiberg–Witten invariants and topology of families of spin 4-manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 15 April 2021, pp. 770-808
- Print publication:
- April 2021
-
- Article
- Export citation
TAUTOLOGICAL RINGS AND STABILISATION
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 17 March 2021, pp. 231-242
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- Export citation