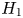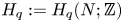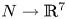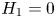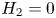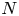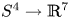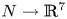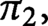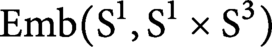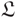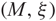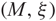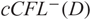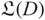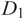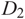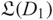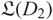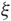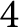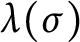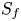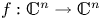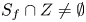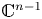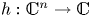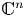Refine listing
Actions for selected content:
163 results in 57Rxx
Orbifold expansion and entire functions with bounded Fatou components
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 5 / May 2022
- Published online by Cambridge University Press:
- 04 March 2021, pp. 1807-1846
- Print publication:
- May 2022
-
- Article
-
- You have access
- Open access
- Export citation
Instantons and Bar-Natan homology
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 22 March 2021, pp. 484-528
- Print publication:
- March 2021
-
- Article
- Export citation
Holomorphic one-forms, fibrations over the circle, and characteristic numbers of Kähler manifolds
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 26 February 2021, pp. 95-103
- Print publication:
- January 2022
-
- Article
-
- You have access
- Open access
- Export citation
Homotopy of gauge groups over high-dimensional manifolds
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 05 February 2021, pp. 182-208
- Print publication:
- February 2022
-
- Article
- Export citation
Embeddings of non-simply-connected 4-manifolds in 7-space. II. On the smooth classification
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 22 January 2021, pp. 163-181
- Print publication:
- February 2022
-
- Article
- Export citation
LOSIK CLASSES FOR CODIMENSION-ONE FOLIATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 08 January 2021, pp. 1391-1419
- Print publication:
- July 2022
-
- Article
- Export citation
Steady Euler flows and Beltrami fields in high dimensions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 07 December 2020, pp. 3610-3633
- Print publication:
- December 2021
-
- Article
- Export citation
Tropically constructed Lagrangians in mirror quintic threefolds
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 20 November 2020, e58
-
- Article
-
- You have access
- Open access
- Export citation
Equivariant cohomology of torus orbifolds
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 20 November 2020, pp. 299-328
- Print publication:
- April 2022
-
- Article
- Export citation
Dynamical incoherence for a large class of partially hyperbolic diffeomorphisms
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 03 November 2020, pp. 3227-3243
- Print publication:
- November 2021
-
- Article
- Export citation
Envelopes of families of framed surfaces and singular solutions of first-order partial differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 15 September 2020, pp. 1515-1542
- Print publication:
- October 2021
-
- Article
- Export citation
Spaces of knotted circles and exotic smooth structures
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 24 August 2020, pp. 1-23
- Print publication:
- February 2022
-
- Article
-
- You have access
- Open access
- Export citation
AN INVARIANT OF LEGENDRIAN AND TRANSVERSE LINKS FROM OPEN BOOK DECOMPOSITIONS OF CONTACT 3-MANIFOLDS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 04 August 2020, pp. 451-483
- Print publication:
- May 2021
-
- Article
- Export citation
Geography of simply connected nonspin symplectic 4-manifolds with positive signature. II
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 10 July 2020, pp. 418-428
- Print publication:
- June 2021
-
- Article
- Export citation
CYCLIC BRANCHED COVERINGS OF BRIESKORN SPHERES BOUNDING ACYCLIC 4-MANIFOLDS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 03 July 2020, pp. 400-413
- Print publication:
- May 2021
-
- Article
- Export citation
A FAST ALGORITHM FOR CALCULATING S-INVARIANTS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 29 June 2020, pp. 378-399
- Print publication:
- May 2021
-
- Article
- Export citation
A certain structure of Artin groups and the isomorphism conjecture
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 21 May 2020, pp. 1153-1170
- Print publication:
- August 2021
-
- Article
- Export citation
On topological approaches to the Jacobian conjecture in ℂn
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 3 / August 2020
- Published online by Cambridge University Press:
- 07 May 2020, pp. 666-675
-
- Article
- Export citation
GENERATORS, RELATIONS, AND HOMOLOGY FOR OZSVÁTH–SZABÓ’S KAUFFMAN-STATES ALGEBRAS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 244 / December 2021
- Published online by Cambridge University Press:
- 17 April 2020, pp. 60-118
- Print publication:
- December 2021
-
- Article
- Export citation
On Steenrod 𝕃-homology, generalized manifolds, and surgery
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 20 March 2020, pp. 579-607
-
- Article
- Export citation