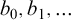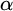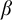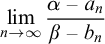Refine listing
Actions for selected content:
170 results in 03DXX
The subTuring degrees
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 17 December 2025, pp. 1-26
-
- Article
- Export citation
A SHORT NOTE ON THE SIGNIFICANCE OF THE PENROSE-HALTING THEOREM
- Part of
-
- Journal:
- Bulletin of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 December 2025, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DECOMPOSITION OF GÖDEL NUMBERINGS INTO MINIMAL NUMBERINGS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 24 November 2025, pp. 1-19
-
- Article
- Export citation
Computability of Brjuno-like functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 12 November 2025, pp. 1-41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE WEAKNESS OF FINDING DESCENDING SEQUENCES IN ILL-FOUNDED LINEAR ORDERS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 29 October 2025, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXTENDING THE BARMPALIAS–LEWIS-PYE LIMIT THEOREM TO ALL REALS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 28 October 2025, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RATE OF CONVERGENCE OF COMPUTABLE PREDICTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 15 October 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE ARITHMETICAL COMPLEXITY OF MODELS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 10 October 2025, pp. 1-10
-
- Article
- Export citation
ON EFFECTIVE CONSTRUCTIONS OF EXISTENTIALLY CLOSED GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 25 September 2025, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LOW
 $_2$ COMPUTABLY ENUMERABLE SETS HAVE HYPERHYPERSIMPLE SUPERSETS
$_2$ COMPUTABLY ENUMERABLE SETS HAVE HYPERHYPERSIMPLE SUPERSETS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 23 September 2025, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE COMPUTABILITY OF OPTIMAL SCOTT SENTENCES
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 17 September 2025, pp. 1-20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ALGORITHMICALLY FINITE, UNIVERSAL, AND
 $*$-UNIVERSAL GROUPS
$*$-UNIVERSAL GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 September 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LATTICE EMBEDDINGS AND PUNCTUAL LINEAR ORDERS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 01 August 2025, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RAMSEY-LIKE THEOREMS FOR THE SCHREIER BARRIER
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 17 July 2025, pp. 1-29
-
- Article
- Export citation
ON REPRESENTATIONS OF IRRATIONAL NUMBERS AND THE COMPUTATIONAL COMPLEXITY OF CONVERTING BETWEEN SUCH REPRESENTATIONS
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 31 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 03 July 2025, pp. 515-589
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RELATIVE LEFTMOST PATH PRINCIPLES AND OMEGA-MODEL REFLECTIONS OF TRANSFINITE INDUCTIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 09 June 2025, pp. 1-15
-
- Article
- Export citation
COMPUTABLE TYPE OF CERTAIN QUOTIENT SPACES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1480-1510
- Print publication:
- December 2025
-
- Article
- Export citation
COUNTEREXAMPLES IN EFFECTIVE TOPOLOGY
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 24 March 2025, pp. 1-24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN ORDER ANALYSIS OF HYPERFINITE BOREL EQUIVALENCE RELATIONS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 21 March 2025, pp. 1-23
-
- Article
- Export citation
On the algorithmic descriptive complexity of attractors in topological dynamics
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 8 / August 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 2533-2560
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation