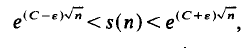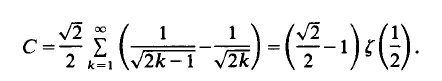Refine listing
Actions for selected content:
336 results in 11Bxx
Bh [g] sequences
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 109-115
- Print publication:
- December 2000
-
- Article
- Export citation
Apéry sequences and legendre transforms
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 68 / Issue 3 / June 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 349-356
- Print publication:
- June 2000
-
- Article
-
- You have access
- Export citation
On the scarcity of powerful binomial coefficients
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 2 / December 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 397-410
- Print publication:
- December 1999
-
- Article
- Export citation
Estimates of the least prime factor of a binomial coefficient
- Part of
-
- Journal:
- Mathematika / Volume 46 / Issue 1 / June 1999
- Published online by Cambridge University Press:
- 26 February 2010, pp. 41-55
- Print publication:
- June 1999
-
- Article
- Export citation
On strings of consecutive integers with no large prime factors
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 2 / April 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 266-276
- Print publication:
- April 1998
-
- Article
-
- You have access
- Export citation
On a conjecture of Crittenden and Vanden Eynden concerning coverings by arithmetic progressions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 63 / Issue 3 / December 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 396-420
- Print publication:
- December 1997
-
- Article
-
- You have access
- Export citation
Bigger and better subset-sum-distinct sets
- Part of
-
- Journal:
- Mathematika / Volume 44 / Issue 1 / June 1997
- Published online by Cambridge University Press:
- 26 February 2010, pp. 56-60
- Print publication:
- June 1997
-
- Article
- Export citation
Explicit bounds on exponential sums and the scarcity of squarefree binomial coefficients
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 1 / June 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 73-107
- Print publication:
- June 1996
-
- Article
- Export citation
On a question of regarding visibility of lattice points
- Part of
-
- Journal:
- Mathematika / Volume 43 / Issue 1 / June 1996
- Published online by Cambridge University Press:
- 26 February 2010, pp. 155-158
- Print publication:
- June 1996
-
- Article
- Export citation
Recurring-with-carry sequences
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 32 / Issue 4 / December 1995
- Published online by Cambridge University Press:
- 14 July 2016, pp. 966-971
- Print publication:
- December 1995
-
- Article
- Export citation
Legendre transforms and Apéry's sequences
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 3 / June 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 358-375
- Print publication:
- June 1995
-
- Article
-
- You have access
- Export citation
On recursive solutions of a unit fraction equation
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 3 / December 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 341-356
- Print publication:
- December 1994
-
- Article
-
- You have access
- Export citation
The number of zero sums modulo m in a sequence of length n
- Part of
-
- Journal:
- Mathematika / Volume 41 / Issue 1 / June 1994
- Published online by Cambridge University Press:
- 26 February 2010, pp. 149-163
- Print publication:
- June 1994
-
- Article
- Export citation
Characterization of two-distance sequences
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 53 / Issue 2 / October 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 198-218
- Print publication:
- October 1992
-
- Article
-
- You have access
- Export citation
An asymptotic formula for a-th powers dividing binomial coefficients
- Part of
-
- Journal:
- Mathematika / Volume 39 / Issue 1 / June 1992
- Published online by Cambridge University Press:
- 26 February 2010, pp. 25-36
- Print publication:
- June 1992
-
- Article
- Export citation
Rational solutions of linear differential equations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 46 / Issue 2 / April 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 184-196
- Print publication:
- April 1989
-
- Article
-
- You have access
- Export citation
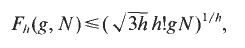
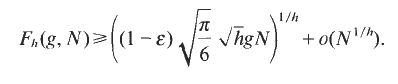
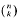 with 3≤
with 3≤ . Unconditionally, it is shown that there are
. Unconditionally, it is shown that there are 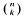 are >
are >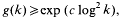
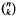 must be highly composite in that it contains many prime factors and often to high powers. It is therefore of interest to enquire as to how infrequently
must be highly composite in that it contains many prime factors and often to high powers. It is therefore of interest to enquire as to how infrequently 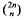 is not squarefree once
is not squarefree once 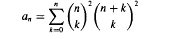
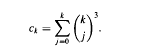
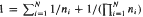 and discuss techniques for generating solutions. By examining a quadratic recurrence relation modulo a family of primes we have found some 500 new infinite sequences of solutions. We also initiate an investigation of the randomness of the distribution of solutions, and show that there are infinitely many solutions not generated by the aforementioned technique.
and discuss techniques for generating solutions. By examining a quadratic recurrence relation modulo a family of primes we have found some 500 new infinite sequences of solutions. We also initiate an investigation of the randomness of the distribution of solutions, and show that there are infinitely many solutions not generated by the aforementioned technique.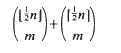
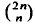 satisfies for arbitrary
satisfies for arbitrary