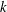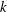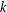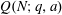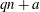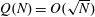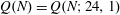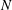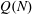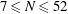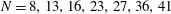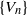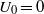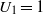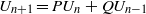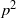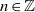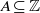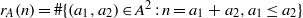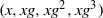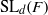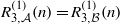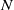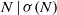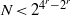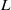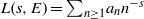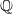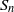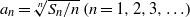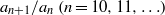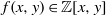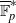Refine listing
Actions for selected content:
336 results in 11Bxx
A FAMILY OF MULTIPLE HARMONIC SUM AND MULTIPLE ZETA STAR VALUE IDENTITIES
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 28 May 2014, pp. 63-71
- Print publication:
- January 2015
-
- Article
- Export citation
THE MINIMAL GROWTH OF A
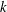 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}k$-REGULAR SEQUENCE
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}k$-REGULAR SEQUENCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 22 May 2014, pp. 195-203
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
AN EFFICIENT METHOD FOR IMPROVING THE COMPUTATIONAL PERFORMANCE OF THE CUBIC LUCAS CRYPTOSYSTEM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 10 April 2014, pp. 160-171
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
On a conjecture of Rudin on squares in arithmetic progressions
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 17 / Issue 1 / 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 58-76
-
- Article
-
- You have access
- Export citation
THE SQUARE TERMS IN GENERALIZED LUCAS SEQUENCES
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 19 December 2013, pp. 85-100
- Print publication:
- January 2014
-
- Article
- Export citation
POLYNOMIAL EQUIVALENCE OF FINITE RINGS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 01 April 2014, pp. 244-257
- Print publication:
- April 2014
-
- Article
-
- You have access
- Export citation
UNIQUE REPRESENTATION BI-BASIS FOR THE INTEGERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 12 September 2013, pp. 460-465
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
MIXING FOR PROGRESSIONS IN NONABELIAN GROUPS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 1 / 2013
- Published online by Cambridge University Press:
- 29 August 2013, e2
-
- Article
-
- You have access
- Open access
- Export citation
A removal lemma for linear configurations in subsets of the circle
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 3 / October 2013
- Published online by Cambridge University Press:
- 28 June 2013, pp. 657-666
-
- Article
-
- You have access
- Export citation
SETS WITH ALMOST COINCIDING REPRESENTATION FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 28 June 2013, pp. 97-111
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
IMPROVED UPPER BOUNDS FOR ODD MULTIPERFECT NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 12 June 2013, pp. 353-359
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
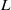 $L$-FUNCTIONS OF ELLIPTIC CURVES AND BINARY RECURRENCES
$L$-FUNCTIONS OF ELLIPTIC CURVES AND BINARY RECURRENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 22 March 2013, pp. 509-519
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
ON NEAR-PERFECT NUMBERS WITH TWO DISTINCT PRIME FACTORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 11 March 2013, pp. 520-524
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
THE UNIVERSAL KUMMER CONGRUENCES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 94 / Issue 1 / February 2013
- Published online by Cambridge University Press:
- 22 March 2013, pp. 106-132
- Print publication:
- February 2013
-
- Article
-
- You have access
- Export citation
ON A SEQUENCE INVOLVING SUMS OF PRIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 18 January 2013, pp. 197-205
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
A linear recurrence sequence of composite numbers
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 November 2012, pp. 360-373
-
- Article
-
- You have access
- Export citation
ELEMENTS OF LARGE ORDER IN PRIME FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 16 October 2012, pp. 169-176
- Print publication:
- August 2013
-
- Article
-
- You have access
- Export citation
A VARIANT OF HOFSTADTER’S SEQUENCE AND FINITE AUTOMATA
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 03 May 2013, pp. 1-8
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
TWIN SQUAREFUL NUMBERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 19 September 2012, pp. 43-51
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
ON DIVISIBILITY OF BINOMIAL COEFFICIENTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 19 September 2012, pp. 189-201
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation