Refine listing
Actions for selected content:
336 results in 11Bxx
ON THE NUMBER OF LATIN RECTANGLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 1 / August 2010
- Published online by Cambridge University Press:
- 22 June 2010, pp. 167-170
- Print publication:
- August 2010
-
- Article
-
- You have access
- Export citation
A NOTE ON A RESULT OF RUZSA, II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 18 June 2010, pp. 340-347
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
ON A NONABELIAN BALOG–SZEMERÉDI-TYPE LEMMA
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 1 / August 2010
- Published online by Cambridge University Press:
- 08 June 2010, pp. 127-132
- Print publication:
- August 2010
-
- Article
-
- You have access
- Export citation
Approximate groups. I The torsion-free nilpotent case
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 10 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 02 June 2010, pp. 37-57
- Print publication:
- January 2011
-
- Article
- Export citation
EULER NUMBERS MODULO 2n
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 09 April 2010, pp. 221-231
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
ON m-COVERS AND m-SYSTEMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 05 October 2009, pp. 223-235
- Print publication:
- April 2010
-
- Article
-
- You have access
- Export citation
FLAT PRIMES AND THIN PRIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 26 April 2010, pp. 282-292
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
Perfect powers from products of consecutive terms in arithmetic progression
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 4 / July 2009
- Published online by Cambridge University Press:
- 01 July 2009, pp. 845-864
- Print publication:
- July 2009
-
- Article
-
- You have access
- Export citation
EIGHT CONSECUTIVE POSITIVE ODD NUMBERS NONE OF WHICH CAN BE EXPRESSED AS A SUM OF TWO PRIME POWERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 80 / Issue 2 / October 2009
- Published online by Cambridge University Press:
- 08 June 2009, pp. 237-243
- Print publication:
- October 2009
-
- Article
-
- You have access
- Export citation
ON THE LARGEST PRIME FACTOR OF THE MERSENNE NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 79 / Issue 3 / June 2009
- Published online by Cambridge University Press:
- 17 April 2009, pp. 455-463
- Print publication:
- June 2009
-
- Article
-
- You have access
- Export citation
Three-term arithmetic progressions and sumsets
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 52 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 02 February 2009, pp. 211-233
-
- Article
-
- You have access
- Export citation
On the Littlewood Problem Modulo a Prime
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 61 / Issue 1 / 01 February 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 141-164
- Print publication:
- 01 February 2009
-
- Article
-
- You have access
- Export citation
A NOTE ON THE FREIMAN AND BALOG–SZEMERÉDI–GOWERS THEOREMS IN FINITE FIELDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 86 / Issue 1 / February 2009
- Published online by Cambridge University Press:
- 01 February 2009, pp. 61-74
- Print publication:
- February 2009
-
- Article
-
- You have access
- Export citation
ON THE DENSITY OF INTEGERS OF THE FORM (p−1)2−n IN ARITHMETIC PROGRESSIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 431-436
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
SUMS OF MULTIPLICATIVE FUNCTIONS OVER A BEATTY SEQUENCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 2 / October 2008
- Published online by Cambridge University Press:
- 01 October 2008, pp. 327-334
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
A NOTE ON A RESULT OF RUZSA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 1 / February 2008
- Published online by Cambridge University Press:
- 01 February 2008, pp. 91-98
- Print publication:
- February 2008
-
- Article
-
- You have access
- Export citation
An Improvement of a Large Sieve Inequality in High Dimensions
- Part of
-
- Journal:
- Mathematika / Volume 52 / Issue 1-2 / December 2005
- Published online by Cambridge University Press:
- 21 December 2009, pp. 93-100
- Print publication:
- December 2005
-
- Article
- Export citation
On a problem of Granville and Zhu Regarding Pascal's triangle
- Part of
-
- Journal:
- Mathematika / Volume 51 / Issue 1-2 / December 2004
- Published online by Cambridge University Press:
- 26 February 2010, pp. 63-82
- Print publication:
- December 2004
-
- Article
- Export citation
Character sums and the series L(1, χ)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 70 / Issue 3 / June 2001
- Published online by Cambridge University Press:
- 09 April 2009, pp. 425-436
- Print publication:
- June 2001
-
- Article
-
- You have access
- Export citation
Combinatorics and linear algebra of Freiman's isomorphism
- Part of
-
- Journal:
- Mathematika / Volume 47 / Issue 1-2 / December 2000
- Published online by Cambridge University Press:
- 26 February 2010, pp. 39-51
- Print publication:
- December 2000
-
- Article
- Export citation
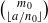 subsets
subsets 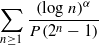
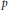
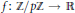
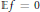
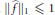
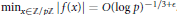
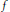
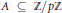
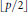
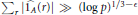
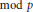
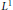

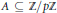
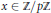
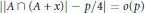
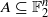 is such that ∣
is such that ∣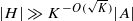 such that
such that 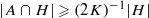 . Under the assumption that
. Under the assumption that  and
and 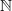 . Erdös and Turán conjectured that, for any basis
. Erdös and Turán conjectured that, for any basis 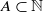 for which
for which 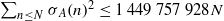 for large enough
for large enough 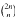 ends with
ends with 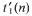 of classes of such cardinality
of classes of such cardinality 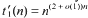 .
.