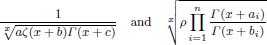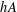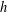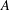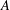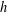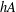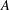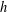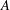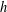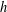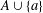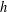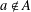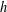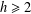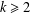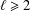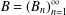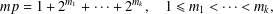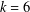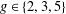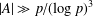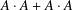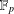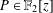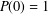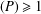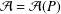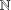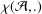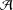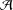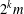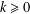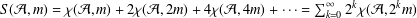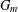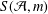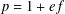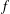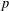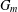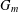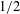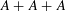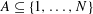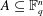Refine listing
Actions for selected content:
336 results in 11Bxx
PARTITIONS OF THE SET OF NONNEGATIVE INTEGERS WITH THE SAME REPRESENTATION FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 04 October 2017, pp. 200-206
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
Log-concavity and strong q-log-convexity for Riordan arrays and recursive matrices
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 6 / December 2017
- Published online by Cambridge University Press:
- 14 August 2017, pp. 1297-1310
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
MULTI-POLY-BERNOULLI NUMBERS AND RELATED ZETA FUNCTIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 232 / December 2018
- Published online by Cambridge University Press:
- 08 May 2017, pp. 19-54
- Print publication:
- December 2018
-
- Article
-
- You have access
- HTML
- Export citation
ON ADDITIVE REPRESENTATION FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 02 May 2017, pp. 380-388
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
ON THE TENTH-ORDER MOCK THETA FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 02 March 2017, pp. 44-62
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
Geometric-progression-free sets over quadratic number fields
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 27 February 2017, pp. 245-262
- Print publication:
- April 2017
-
- Article
- Export citation
MONOTONIC PHINOMIAL COEFFICIENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 09 January 2017, pp. 365-372
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
THE QUOTIENT SET OF
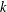 $k$ -GENERALISED FIBONACCI NUMBERS IS DENSE IN
$k$ -GENERALISED FIBONACCI NUMBERS IS DENSE IN 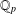 $\mathbb{Q}_{p}$
$\mathbb{Q}_{p}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 09 January 2017, pp. 24-29
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
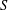 $S$ -PARTS OF TERMS OF INTEGER LINEAR RECURRENCE SEQUENCES
$S$ -PARTS OF TERMS OF INTEGER LINEAR RECURRENCE SEQUENCES
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 840-851
- Print publication:
- 2017
-
- Article
- Export citation
NEW BOUNDS FOR SZEMERÉDI’S THEOREM, III: A POLYLOGARITHMIC BOUND FOR
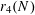 $r_{4}(N)$
$r_{4}(N)$
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 944-1040
- Print publication:
- 2017
-
- Article
-
- You have access
- HTML
- Export citation
ON SOME MULTIPLE CHARACTER SUMS
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 03 April 2017, pp. 553-560
- Print publication:
- 2017
-
- Article
- Export citation
The Monotonicity and Log-Behaviour of Some Functions Related to the Euler Gamma Function
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 09 November 2016, pp. 527-543
-
- Article
- Export citation
ON POLY-EULER NUMBERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 03 November 2016, pp. 126-144
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
A NOTE ON ASYMPTOTIC NONBASES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 13 October 2016, pp. 1-4
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
PERFECT POWERS IN PRODUCTS OF TERMS OF ELLIPTIC DIVISIBILITY SEQUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 3 / December 2016
- Published online by Cambridge University Press:
- 21 July 2016, pp. 395-404
- Print publication:
- December 2016
-
- Article
-
- You have access
- Export citation
ALMOST ALL PRIMES HAVE A MULTIPLE OF SMALL HAMMING WEIGHT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 23 May 2016, pp. 224-235
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
On Systems of Complexity One in the Primes
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 10 May 2016, pp. 133-163
-
- Article
- Export citation
On Euler's function
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 146 / Issue 4 / August 2016
- Published online by Cambridge University Press:
- 19 April 2016, pp. 769-775
- Print publication:
- August 2016
-
- Article
- Export citation
SETS WITH EVEN PARTITION FUNCTIONS AND CYCLOTOMIC NUMBERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 3 / June 2016
- Published online by Cambridge University Press:
- 14 March 2016, pp. 289-302
- Print publication:
- June 2016
-
- Article
-
- You have access
- Export citation
ROTH’S THEOREM FOR FOUR VARIABLES AND ADDITIVE STRUCTURES IN SUMS OF SPARSE SETS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 19 February 2016, e5
-
- Article
-
- You have access
- Open access
- Export citation
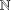
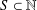
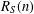
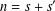
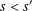
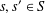
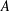
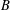
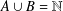
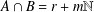
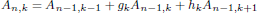
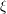
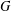
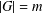
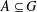
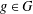
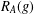
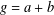
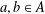
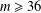
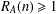
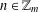
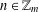
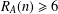
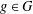
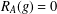
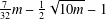
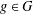
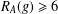
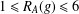
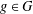
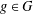
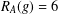
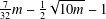
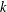
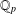
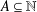
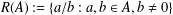
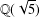
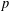
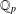
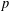
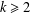
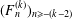
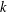
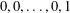
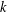
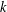
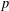
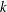
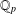
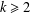
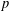
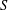
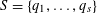
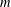
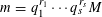
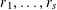
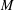
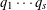
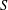
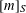
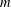
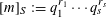
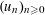
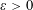
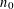
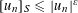
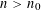
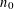
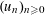
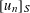
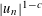

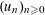
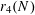
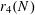
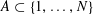
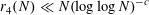
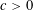
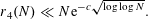
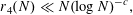
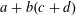
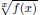 is given, which is a continuous analogue of a result of Wang and Zhu. On the other hand, the log-behaviour of the functions
is given, which is a continuous analogue of a result of Wang and Zhu. On the other hand, the log-behaviour of the functions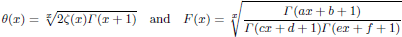
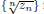 for some combinatorial sequences (including the Bernoulli numbers, the tangent numbers, the Catalan numbers, the Fuss–Catalan numbers, and the binomial coefficients
for some combinatorial sequences (including the Bernoulli numbers, the tangent numbers, the Catalan numbers, the Fuss–Catalan numbers, and the binomial coefficients 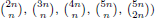 are demonstrated. In particular, this contains some results of Chen
are demonstrated. In particular, this contains some results of Chen 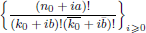
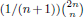 and the central binomial coefficients
and the central binomial coefficients 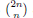 are infinitely log-monotonic, and strengthens one result of Su and Wang that
are infinitely log-monotonic, and strengthens one result of Su and Wang that 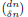 is log-convex in
is log-convex in