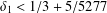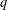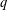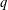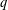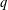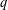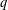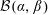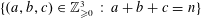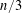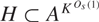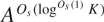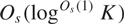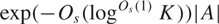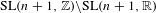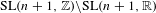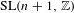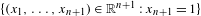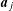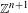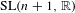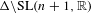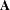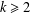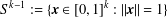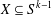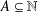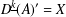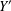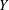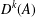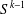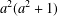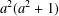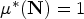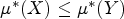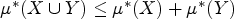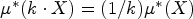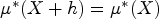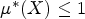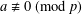Refine listing
Actions for selected content:
336 results in 11Bxx
LINEAR RELATIONS AND INTEGRABILITY FOR CLUSTER ALGEBRAS FROM AFFINE QUIVERS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 13 August 2020, pp. 584-621
- Print publication:
- September 2021
-
- Article
- Export citation
On finite sets of small tripling or small alternation in arbitrary groups
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 29 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 30 June 2020, pp. 807-829
-
- Article
- Export citation
SUM-PRODUCT ESTIMATES FOR DIAGONAL MATRICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 24 June 2020, pp. 28-37
- Print publication:
- February 2021
-
- Article
- Export citation
Möbius Randomness Law for Frobenius Traces of Ordinary Curves
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 15 May 2020, pp. 192-203
- Print publication:
- March 2021
-
- Article
- Export citation
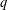 $q$-DEFORMED RATIONALS AND
$q$-DEFORMED RATIONALS AND 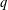 $q$-CONTINUED FRACTIONS
$q$-CONTINUED FRACTIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 06 March 2020, e13
-
- Article
-
- You have access
- Open access
- Export citation
Automorphisms of automatic shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 20 February 2020, pp. 1530-1559
- Print publication:
- May 2021
-
- Article
- Export citation
PROOF OF TWO CONJECTURES ON SUPERCONGRUENCES INVOLVING CENTRAL BINOMIAL COEFFICIENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 13 February 2020, pp. 360-364
- Print publication:
- December 2020
-
- Article
- Export citation
DEGREE-ONE MAHLER FUNCTIONS: ASYMPTOTICS, APPLICATIONS AND SPECULATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 05 February 2020, pp. 399-409
- Print publication:
- December 2020
-
- Article
- Export citation
CLOSED FORMS FOR DEGENERATE BERNOULLI POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 10 January 2020, pp. 207-217
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
SOME REMARKS ON MINIMAL ASYMPTOTIC BASES OF ORDER THREE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 21-30
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Irregularities in the Distribution of Prime Numbers in a Beatty Sequence
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 16 December 2019, pp. 738-743
- Print publication:
- December 2020
-
- Article
- Export citation
A DISTRIBUTION ON TRIPLES WITH MAXIMUM ENTROPY MARGINAL
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 09 December 2019, e46
-
- Article
-
- You have access
- Open access
- Export citation
LOWER BOUNDS FOR PERIODS OF DUCCI SEQUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 22 November 2019, pp. 31-38
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Polylogarithmic bounds in the nilpotent Freiman theorem
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 08 October 2019, pp. 111-127
- Print publication:
- January 2021
-
- Article
- Export citation
Equidistribution of Farey sequences on horospheres in covers of
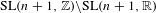 $\text{SL}(n+1,\mathbb{Z})\backslash \text{SL}(n+1,\mathbb{R})$ and applications
$\text{SL}(n+1,\mathbb{Z})\backslash \text{SL}(n+1,\mathbb{R})$ and applications
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 2 / February 2021
- Published online by Cambridge University Press:
- 07 October 2019, pp. 471-493
- Print publication:
- February 2021
-
- Article
- Export citation
DIRECTIONS SETS: A GENERALISATION OF RATIO SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 13 September 2019, pp. 389-395
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
GAPS BETWEEN DIVISIBLE TERMS IN
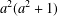 $a^{2}(a^{2}+1)$
$a^{2}(a^{2}+1)$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 13 September 2019, pp. 396-400
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
Automaticity and Invariant Measures of Linear Cellular Automata
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 05 September 2019, pp. 1691-1726
- Print publication:
- December 2020
-
- Article
- Export citation
On the notions of upper and lower density
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 30 August 2019, pp. 139-167
-
- Article
- Export citation
NEW SUPERCONGRUENCES INVOLVING PRODUCTS OF TWO BINOMIAL COEFFICIENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 23 August 2019, pp. 367-378
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation