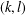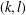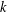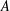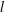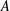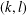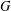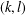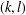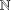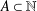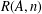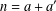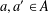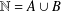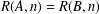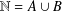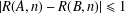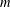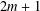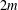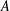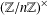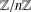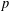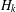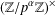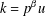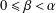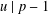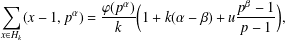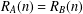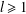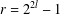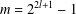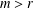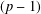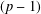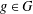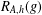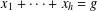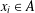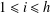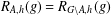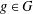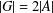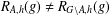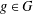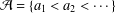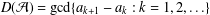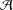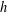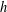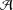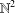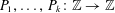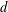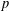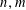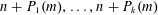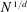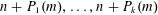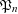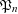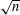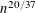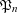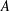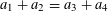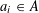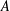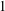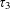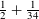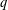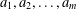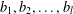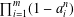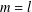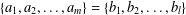Refine listing
Actions for selected content:
336 results in 11Bxx
THE MAXIMUM SIZE OF
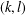 $(k,l)$-SUM-FREE SETS IN CYCLIC GROUPS
$(k,l)$-SUM-FREE SETS IN CYCLIC GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 26 December 2018, pp. 184-194
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
ANALOGUES OF THE AOKI–OHNO AND LE–MURAKAMI RELATIONS FOR FINITE MULTIPLE ZETA VALUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 26 December 2018, pp. 34-40
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
ON PARTITIONS OF NONNEGATIVE INTEGERS AND REPRESENTATION FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 11 December 2018, pp. 385-387
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
A NEW MENON’S IDENTITY FROM GROUP ACTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 28 November 2018, pp. 369-375
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
ON A PROBLEM OF CHEN AND LEV
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 28 November 2018, pp. 15-22
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
IDEAL CHAINS IN RESIDUALLY FINITE DEDEKIND DOMAINS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 28 November 2018, pp. 56-67
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
CONGRUENCES FOR THE
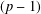 $(p-1)$TH APÉRY NUMBER
$(p-1)$TH APÉRY NUMBER
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 28 November 2018, pp. 362-368
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Szemerédi's Theorem in the Primes
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 19 November 2018, pp. 443-457
-
- Article
- Export citation
ON NUMBERS
 $n$ WITH POLYNOMIAL IMAGE COPRIME WITH THE
$n$ WITH POLYNOMIAL IMAGE COPRIME WITH THE  $n$TH TERM OF A LINEAR RECURRENCE
$n$TH TERM OF A LINEAR RECURRENCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 28 August 2018, pp. 23-33
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
REPRESENTATION FUNCTIONS ON ABELIAN GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 15 August 2018, pp. 10-14
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
On the General Solution of the Heideman–Hogan Family of Recurrences
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 14 August 2018, pp. 1113-1125
-
- Article
- Export citation
A NOTE ON THE ERDŐS–GRAHAM THEOREM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 23 April 2018, pp. 363-366
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
VISIBLE POINTS ON EXPONENTIAL CURVES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 07 March 2018, pp. 353-359
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
FINITELY STABLE ADDITIVE BASES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 20 February 2018, pp. 360-362
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
POLYNOMIAL PATTERNS IN THE PRIMES
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 6 / 2018
- Published online by Cambridge University Press:
- 12 February 2018, e1
-
- Article
-
- You have access
- Open access
- Export citation
DENOMINATORS OF BERNOULLI POLYNOMIALS
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 2 / 2018
- Published online by Cambridge University Press:
- 16 April 2018, pp. 519-541
- Print publication:
- 2018
-
- Article
- Export citation
ADDITIVE ENERGY AND THE METRIC POISSONIAN PROPERTY
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 3 / 2018
- Published online by Cambridge University Press:
- 19 June 2018, pp. 679-700
- Print publication:
- 2018
-
- Article
- Export citation
TERNARY DIVISOR FUNCTIONS IN ARITHMETIC PROGRESSIONS TO SMOOTH MODULI
- Part of
-
- Journal:
- Mathematika / Volume 64 / Issue 3 / 2018
- Published online by Cambridge University Press:
- 19 June 2018, pp. 701-729
- Print publication:
- 2018
-
- Article
- Export citation
Arithmetic properties of Apéry-like numbers
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 2 / February 2018
- Published online by Cambridge University Press:
- 20 October 2017, pp. 249-274
- Print publication:
- February 2018
-
- Article
- Export citation
NOTE ON LEHMER–PIERCE SEQUENCES WITH THE SAME PRIME DIVISORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 04 October 2017, pp. 11-14
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation