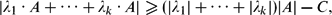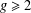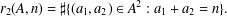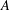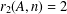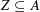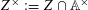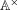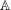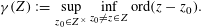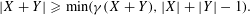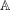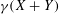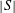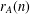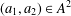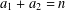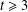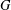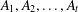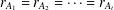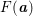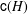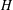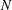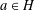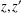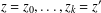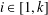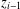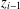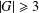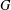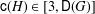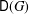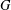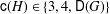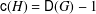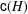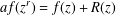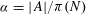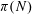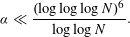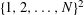Refine listing
Actions for selected content:
336 results in 11Bxx
A UNIQUE REPRESENTATION BI-BASIS FOR THE INTEGERS. II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 1 / August 2016
- Published online by Cambridge University Press:
- 08 January 2016, pp. 1-6
- Print publication:
- August 2016
-
- Article
-
- You have access
- Export citation
ARITHMETIC PROGRESSIONS IN SETS OF SMALL DOUBLING
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 17 February 2016, pp. 587-613
- Print publication:
- 2016
-
- Article
- Export citation
WARING’S PROBLEM WITH PIATETSKI-SHAPIRO NUMBERS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 17 February 2016, pp. 524-550
- Print publication:
- 2016
-
- Article
- Export citation
On a generalization of a waiting time problem and some combinatorial identities
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 30 March 2016, pp. 981-989
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
ON THE SQUARE-FREE REPRESENTATION FUNCTION OF A NORM FORM AND NILSEQUENCES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 11 November 2015, pp. 107-135
- Print publication:
- February 2018
-
- Article
- Export citation
On n-Sums in an Abelian Group
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 3 / May 2016
- Published online by Cambridge University Press:
- 03 November 2015, pp. 419-435
-
- Article
- Export citation
Ramanujan's Radial Limits and Mixed Mock Modular Bilateral q-Hypergeometric Series
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 59 / Issue 3 / August 2016
- Published online by Cambridge University Press:
- 26 October 2015, pp. 787-799
-
- Article
- Export citation
ADDITIVE DIMENSION AND A THEOREM OF SANDERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 22 October 2015, pp. 124-144
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
On the Number of Bh-Sets
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 1 / January 2016
- Published online by Cambridge University Press:
- 16 September 2015, pp. 108-129
-
- Article
- Export citation
Sum of Many Dilates
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 25 / Issue 3 / May 2016
- Published online by Cambridge University Press:
- 08 September 2015, pp. 460-469
-
- Article
- Export citation
RESOLVABILITY PROPERTIES OF SIMILAR TOPOLOGIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 03 September 2015, pp. 470-477
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
ON MINIMAL ASYMPTOTIC
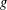 $g$-ADIC BASES
$g$-ADIC BASES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 05 August 2015, pp. 374-379
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
CAUCHY–DAVENPORT TYPE THEOREMS FOR SEMIGROUPS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 22 May 2015, pp. 1-12
- Print publication:
- 2016
-
- Article
- Export citation
ON A PARTITION PROBLEM OF FINITE ABELIAN GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 1 / August 2015
- Published online by Cambridge University Press:
- 29 April 2015, pp. 24-31
- Print publication:
- August 2015
-
- Article
-
- You have access
- Export citation
INFINITE PRODUCTS OF CYCLOTOMIC POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 26 February 2015, pp. 400-411
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
Effective limit distribution of the Frobenius numbers
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 5 / May 2015
- Published online by Cambridge University Press:
- 22 December 2014, pp. 898-916
- Print publication:
- May 2015
-
- Article
- Export citation
THE CATENARY DEGREE OF KRULL MONOIDS II
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 21 November 2014, pp. 324-354
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
ALGEBRAIC INDEPENDENCE OF CERTAIN MAHLER FUNCTIONS AND OF THEIR VALUES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 11 November 2014, pp. 289-310
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
ON IMPROVING ROTH’S THEOREM IN THE PRIMES
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 09 October 2014, pp. 49-62
- Print publication:
- January 2015
-
- Article
- Export citation
MATRIX PROGRESSIONS IN MULTIDIMENSIONAL SETS OF INTEGERS
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 13 August 2014, pp. 14-48
- Print publication:
- January 2015
-
- Article
- Export citation
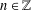
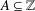
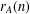
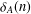
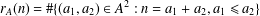
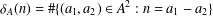
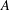
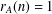
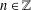
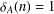
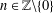
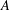
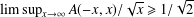
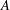
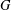
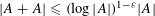
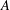
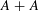
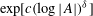
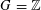
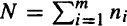 Let
Let