Refine listing
Actions for selected content:
343 results in 11Bxx
 $L$-FUNCTIONS OF ELLIPTIC CURVES AND BINARY RECURRENCES
$L$-FUNCTIONS OF ELLIPTIC CURVES AND BINARY RECURRENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 22 March 2013, pp. 509-519
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
ON NEAR-PERFECT NUMBERS WITH TWO DISTINCT PRIME FACTORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 11 March 2013, pp. 520-524
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
ON A SEQUENCE INVOLVING SUMS OF PRIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 18 January 2013, pp. 197-205
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
A linear recurrence sequence of composite numbers
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 15 / May 2012
- Published online by Cambridge University Press:
- 01 November 2012, pp. 360-373
-
- Article
-
- You have access
- Export citation
ELEMENTS OF LARGE ORDER IN PRIME FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 16 October 2012, pp. 169-176
- Print publication:
- August 2013
-
- Article
-
- You have access
- Export citation
TWIN SQUAREFUL NUMBERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 19 September 2012, pp. 43-51
-
- Article
-
- You have access
- Export citation
ON THE EQUATION f(g(x))=f(x)hm(x) FOR COMPOSITE POLYNOMIALS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 19 September 2012, pp. 155-161
-
- Article
-
- You have access
- Export citation
ON DIVISIBILITY OF BINOMIAL COEFFICIENTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 19 September 2012, pp. 189-201
-
- Article
-
- You have access
- Export citation
ROOTS OF UNITY AS QUOTIENTS OF TWO ROOTS OF A POLYNOMIAL
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 10 August 2012, pp. 137-144
-
- Article
-
- You have access
- Export citation
RATIONAL APPROXIMATIONS TO VALUES OF BELL POLYNOMIALS AT POINTS INVOLVING EULER’S CONSTANT AND ZETA VALUES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 15 June 2012, pp. 71-98
-
- Article
-
- You have access
- Export citation
ALGEBRAIC DIVISIBILITY SEQUENCES OVER FUNCTION FIELDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 24 April 2012, pp. 99-126
-
- Article
-
- You have access
- Export citation
THE LEAST COMMON MULTIPLE OF CONSECUTIVE TERMS IN A QUADRATIC PROGRESSION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 12 April 2012, pp. 389-404
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
On numbers n dividing the nth term of a linear recurrence
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 55 / Issue 2 / June 2012
- Published online by Cambridge University Press:
- 23 February 2012, pp. 271-289
-
- Article
-
- You have access
- Export citation
SOME REMARKS ON THE RIEMANN ZETA FUNCTION AND PRIME FACTORS OF NUMERATORS OF BERNOULLI NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 86 / Issue 2 / October 2012
- Published online by Cambridge University Press:
- 12 December 2011, pp. 216-223
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
ON THE CONSECUTIVE POWERS OF A PRIMITIVE ROOT: GAPS AND EXPONENTIAL SUMS
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 1 / January 2012
- Published online by Cambridge University Press:
- 08 November 2011, pp. 11-20
- Print publication:
- January 2012
-
- Article
- Export citation
AN EXTENSION OF SURY’S IDENTITY AND RELATED CONGRUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 3 / June 2012
- Published online by Cambridge University Press:
- 04 October 2011, pp. 482-496
- Print publication:
- June 2012
-
- Article
-
- You have access
- Export citation
SUMSETS AND DIFFERENCE SETS CONTAINING A COMMON TERM OF A SEQUENCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 26 September 2011, pp. 79-83
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
ON SUM OF PRODUCTS AND THE ERDŐS DISTANCE PROBLEM OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 1 / August 2011
- Published online by Cambridge University Press:
- 21 June 2011, pp. 1-9
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
DENSE SETS OF INTEGERS WITH A PRESCRIBED REPRESENTATION FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 1 / August 2011
- Published online by Cambridge University Press:
- 16 June 2011, pp. 40-43
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
ON A CURIOUS PROPERTY OF BELL NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 84 / Issue 1 / August 2011
- Published online by Cambridge University Press:
- 14 June 2011, pp. 153-158
- Print publication:
- August 2011
-
- Article
-
- You have access
- Export citation
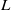
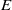
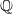
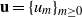
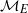

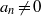
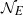
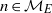
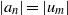
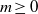
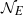
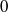
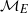

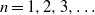
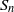

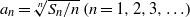
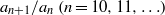
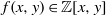
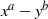
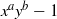
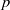
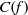
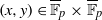
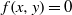
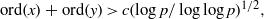

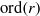

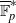
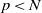
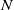
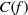
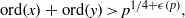
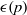
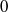
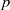
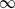
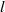

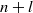

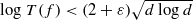 . In the opposite direction, we show that the constant 2cannot be replaced by a number smaller than 1 . These estimates are useful in the study of degenerate and nondegenerate linear recurrence sequences over a number field
. In the opposite direction, we show that the constant 2cannot be replaced by a number smaller than 1 . These estimates are useful in the study of degenerate and nondegenerate linear recurrence sequences over a number field 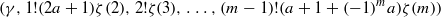
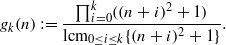
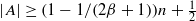 , then (
, then (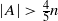 , then (
, then ( cannot be improved.
cannot be improved.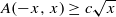 for infinitely many positive integers
for infinitely many positive integers 