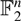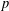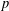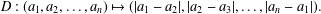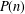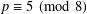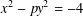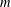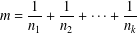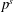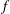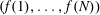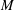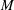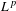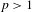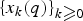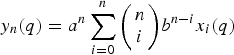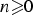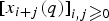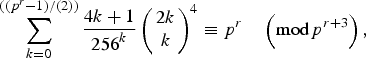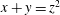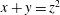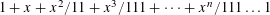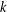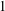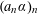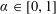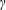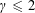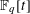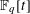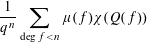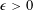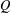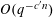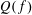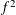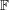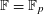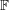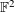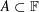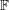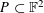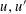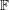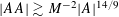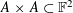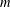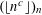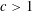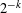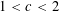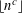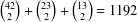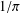Refine listing
Actions for selected content:
336 results in 11Bxx
Triforce and corners
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 1 / July 2020
- Published online by Cambridge University Press:
- 12 July 2019, pp. 209-223
- Print publication:
- July 2020
-
- Article
- Export citation
APPLICATIONS OF LERCH’S THEOREM TO PERMUTATIONS OF QUADRATIC RESIDUES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 10 July 2019, pp. 362-371
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
PERIODS OF DUCCI SEQUENCES AND ODD SOLUTIONS TO A PELLIAN EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 03 July 2019, pp. 201-205
- Print publication:
- October 2019
-
- Article
-
- You have access
- Open access
- Export citation
Automatic Sequences and Generalised Polynomials
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 13 June 2019, pp. 392-426
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
A NOTE ON THE SUM OF RECIPROCALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 17 May 2019, pp. 189-193
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
Büchi’s Problem in Modular Arithmetic for Arbitrary Quadratic Polynomials
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 26 April 2019, pp. 876-885
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Nilsystems and ergodic averages along primes
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 10 / October 2020
- Published online by Cambridge University Press:
- 11 April 2019, pp. 2769-2777
- Print publication:
- October 2020
-
- Article
-
- You have access
- Open access
- Export citation
Entiers friables dans des progressions arithmétiques de grand module
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 1 / July 2020
- Published online by Cambridge University Press:
- 20 March 2019, pp. 75-102
- Print publication:
- July 2020
-
- Article
- Export citation
Positivity and continued fractions from the binomial transformation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 18 March 2019, pp. 831-847
- Print publication:
- June 2019
-
- Article
- Export citation
A LOWER BOUND FOR THE LARGE SIEVE WITH SQUARE MODULI
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 27 February 2019, pp. 225-229
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
Some congruences involving fourth powers of central q-binomial coefficients
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 30 January 2019, pp. 1127-1138
- Print publication:
- June 2020
-
- Article
- Export citation
Asymptotics for some polynomial patterns in the primes
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 17 January 2019, pp. 1241-1290
- Print publication:
- October 2019
-
- Article
- Export citation
Monochromatic Solutions to
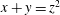 $x+y=z^{2}$
$x+y=z^{2}$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 579-605
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
A CLASS OF IRREDUCIBLE POLYNOMIALS ASSOCIATED WITH PRIME DIVISORS OF VALUES OF CYCLOTOMIC POLYNOMIALS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 4 / 2019
- Published online by Cambridge University Press:
- 14 August 2019, pp. 1033-1037
- Print publication:
- 2019
-
- Article
- Export citation
THERE IS NO KHINTCHINE THRESHOLD FOR METRIC PAIR CORRELATIONS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 4 / 2019
- Published online by Cambridge University Press:
- 23 July 2019, pp. 929-949
- Print publication:
- 2019
-
- Article
- Export citation
INTERVALS BETWEEN CONSECUTIVE NUMBERS WHICH ARE SUMS OF TWO SQUARES
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 4 / 2019
- Published online by Cambridge University Press:
- 14 August 2019, pp. 1018-1032
- Print publication:
- 2019
-
- Article
- Export citation
LINEAR AND QUADRATIC UNIFORMITY OF THE MÖBIUS FUNCTION OVER
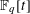 $\mathbb{F}_{q}[t]$
$\mathbb{F}_{q}[t]$
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 05 March 2019, pp. 505-529
- Print publication:
- 2019
-
- Article
- Export citation
NEW RESULTS ON SUM-PRODUCT TYPE GROWTH OVER FIELDS
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 02 April 2019, pp. 588-642
- Print publication:
- 2019
-
- Article
- Export citation
RANDOMNESS AND NON-RANDOMNESS PROPERTIES OF PIATETSKI-SHAPIRO SEQUENCES MODULO
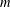 $m$
$m$
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 4 / 2019
- Published online by Cambridge University Press:
- 14 August 2019, pp. 1051-1073
- Print publication:
- 2019
-
- Article
- Export citation
HYPERGEOMETRIC MODULAR EQUATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 107 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 338-366
- Print publication:
- December 2019
-
- Article
-
- You have access
- Open access
- Export citation