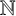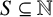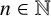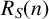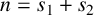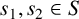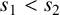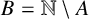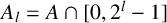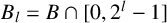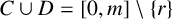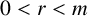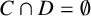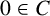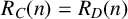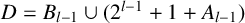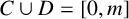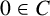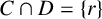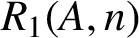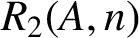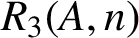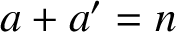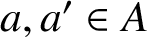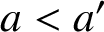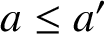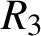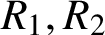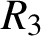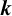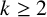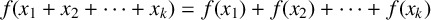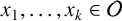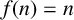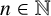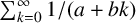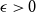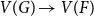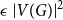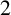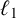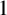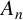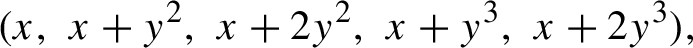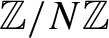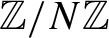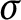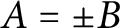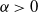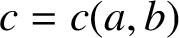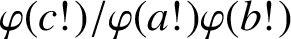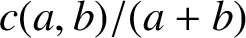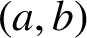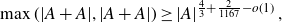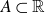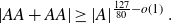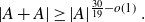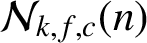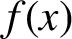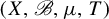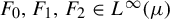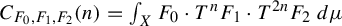Refine listing
Actions for selected content:
343 results in 11Bxx
ON INTEGER SETS WITH THE SAME REPRESENTATION FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 03 March 2022, pp. 224-235
- Print publication:
- October 2022
-
- Article
- Export citation
ON A PROBLEM ABOUT ADDITIVE REPRESENTATION FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 365-371
- Print publication:
- June 2022
-
- Article
- Export citation
ON A
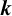 $\boldsymbol {k}$-ADDITIVE UNIQUENESS SET FOR MULTIPLICATIVE FUNCTIONS
$\boldsymbol {k}$-ADDITIVE UNIQUENESS SET FOR MULTIPLICATIVE FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 209-214
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A GENERALISATION OF A THEOREM OF ERDŐS AND NIVEN
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 24 January 2022, pp. 215-223
- Print publication:
- October 2022
-
- Article
- Export citation
Removal lemmas and approximate homomorphisms
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 24 January 2022, pp. 721-736
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ABELIAN DIFFERENCE SETS AS LATTICE COVERINGS AND LATTICE TILINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 24 January 2022, pp. 177-184
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On several notions of complexity of polynomial progressions
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 4 / April 2023
- Published online by Cambridge University Press:
- 20 January 2022, pp. 1269-1323
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On multiplicative energy of subsets of varieties
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 13 January 2022, pp. 322-340
- Print publication:
- February 2023
-
- Article
- Export citation
Kneser’s theorem in
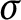 $\sigma $-finite abelian groups
$\sigma $-finite abelian groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 10 January 2022, pp. 936-942
- Print publication:
- December 2022
-
- Article
- Export citation
ON HIGHER DIMENSIONAL ARITHMETIC PROGRESSIONS IN MEYER SETS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 06 December 2021, pp. 312-336
- Print publication:
- June 2023
-
- Article
- Export citation
SZEMERÉDI’S THEOREM: AN EXPLORATION OF IMPURITY, EXPLANATION, AND CONTENT
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 16 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 03 December 2021, pp. 700-739
- Print publication:
- September 2023
-
- Article
- Export citation
A blurred view of Van der Waerden type theorems
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 26 November 2021, pp. 684-701
-
- Article
- Export citation
DENSITY-LIKE AND GENERALIZED DENSITY IDEALS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 23 November 2021, pp. 228-251
- Print publication:
- March 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A restaurant process with cocktail bar and relations to the three-parameter Mittag–Leffler distribution
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 58 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 978-1006
- Print publication:
- December 2021
-
- Article
- Export citation
ON QUOTIENTS OF VALUES OF EULER’S FUNCTION ON FACTORIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 17 November 2021, pp. 353-364
- Print publication:
- June 2022
-
- Article
- Export citation
An update on the sum-product problem
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 2 / September 2022
- Published online by Cambridge University Press:
- 11 October 2021, pp. 411-430
- Print publication:
- September 2022
-
- Article
- Export citation
A FAMILY OF
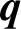 $\boldsymbol {q}$-SUPERCONGRUENCES MODULO THE CUBE OF A CYCLOTOMIC POLYNOMIAL
$\boldsymbol {q}$-SUPERCONGRUENCES MODULO THE CUBE OF A CYCLOTOMIC POLYNOMIAL
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 03 September 2021, pp. 296-302
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SUMS OF POLYNOMIAL-TYPE EXCEPTIONAL UNITS MODULO
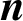 $\boldsymbol {n}$
$\boldsymbol {n}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 21 July 2021, pp. 202-211
- Print publication:
- April 2022
-
- Article
- Export citation
Multiple correlation sequences not approximable by nilsequences
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 9 / September 2022
- Published online by Cambridge University Press:
- 16 July 2021, pp. 2711-2722
- Print publication:
- September 2022
-
- Article
- Export citation
CONTRIBUTIONS TO THE THEORY OF F-AUTOMATIC SETS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 08 June 2021, pp. 127-158
- Print publication:
- March 2022
-
- Article
- Export citation