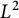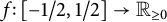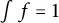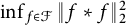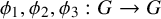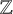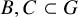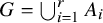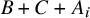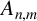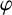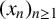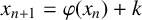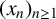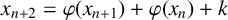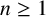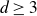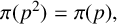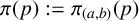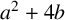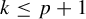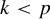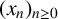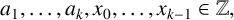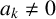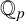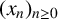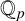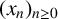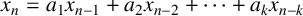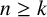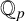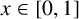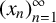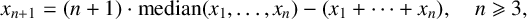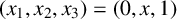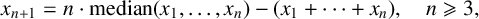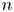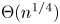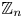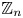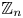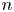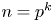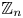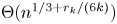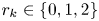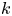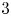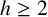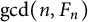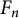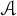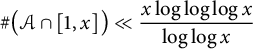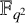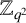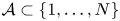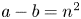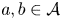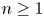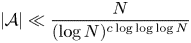Refine listing
Actions for selected content:
336 results in 11Bxx
INFINITE SERIES CONCERNING HARMONIC NUMBERS AND QUINTIC CENTRAL BINOMIAL COEFFICIENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 07 July 2023, pp. 225-241
- Print publication:
- April 2024
-
- Article
- Export citation
An optimal
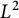 $L^2$ autoconvolution inequality
$L^2$ autoconvolution inequality
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 05 July 2023, pp. 108-121
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bohr sets in sumsets II: countable abelian groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 03 July 2023, e57
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A proof of the Erdős primitive set conjecture
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 14 June 2023, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The first-order theory of binary overlap-free words is decidable
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 26 May 2023, pp. 1144-1162
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE DIVISIBILITY OF SUMS OF q-SUPER CATALAN NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 15 May 2023, pp. 215-224
- Print publication:
- April 2024
-
- Article
- Export citation
ON THE ITERATES OF THE SHIFTED EULER’S FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 12 May 2023, pp. 206-214
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Positive lower density for prime divisors of generic linear recurrences
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 3 / November 2023
- Published online by Cambridge University Press:
- 24 April 2023, pp. 467-478
- Print publication:
- November 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Direct and inverse results for popular differences in trees of positive dimension
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 2 / February 2024
- Published online by Cambridge University Press:
- 05 April 2023, pp. 481-508
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON GENERALISED WALL–SUN–SUN PRIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 28 February 2023, pp. 373-378
- Print publication:
- December 2023
-
- Article
- Export citation
ON NEAR-PERFECT NUMBERS OF SPECIAL FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 14 February 2023, pp. 366-372
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On higher-order Fourier analysis in characteristic p
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 12 / December 2023
- Published online by Cambridge University Press:
- 27 January 2023, pp. 3971-4040
- Print publication:
- December 2023
-
- Article
- Export citation
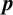 $\boldsymbol {p}$-ADIC QUOTIENT SETS: LINEAR RECURRENCE SEQUENCES
$\boldsymbol {p}$-ADIC QUOTIENT SETS: LINEAR RECURRENCE SEQUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 05 January 2023, pp. 19-28
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE AKIYAMA MEAN-MEDIAN MAP HAS UNBOUNDED TRANSIT TIME AND DISCONTINUOUS LIMIT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 23 November 2022, pp. 298-307
- Print publication:
- October 2023
-
- Article
- Export citation
Discrepancy in modular arithmetic progressions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 01 December 2022, pp. 2082-2108
- Print publication:
- November 2022
-
- Article
- Export citation
ON MINIMAL RESTRICTED ASYMPTOTIC BASES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 06 October 2022, pp. 368-373
- Print publication:
- June 2023
-
- Article
- Export citation
ZAREMBA, SALEM AND THE FRACTAL NATURE OF GHOST DISTRIBUTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 06 October 2022, pp. 374-389
- Print publication:
- June 2023
-
- Article
- Export citation
On the greatest common divisor of n and the nth Fibonacci number, II
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 06 October 2022, pp. 617-625
- Print publication:
- June 2023
-
- Article
- Export citation
ON LINEARISED POLYNOMIALS, SIDON ARRAYS AND FAST CONSTRUCTION OF SIDON SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 30 August 2022, pp. 376-384
- Print publication:
- December 2022
-
- Article
- Export citation
A new upper bound for sets with no square differences
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 30 September 2022, pp. 1777-1798
- Print publication:
- August 2022
-
- Article
- Export citation