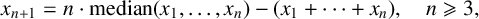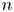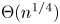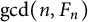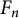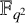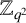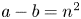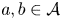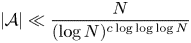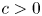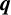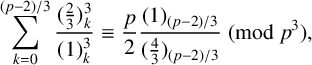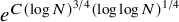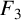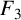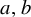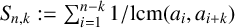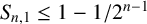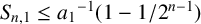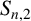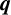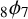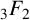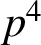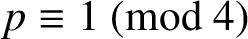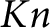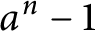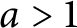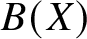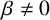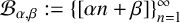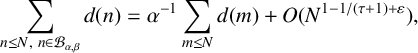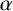Refine listing
Actions for selected content:
343 results in 11Bxx
THE AKIYAMA MEAN-MEDIAN MAP HAS UNBOUNDED TRANSIT TIME AND DISCONTINUOUS LIMIT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 23 November 2022, pp. 298-307
- Print publication:
- October 2023
-
- Article
- Export citation
Discrepancy in modular arithmetic progressions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 01 December 2022, pp. 2082-2108
- Print publication:
- November 2022
-
- Article
- Export citation
ON MINIMAL RESTRICTED ASYMPTOTIC BASES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 06 October 2022, pp. 368-373
- Print publication:
- June 2023
-
- Article
- Export citation
ZAREMBA, SALEM AND THE FRACTAL NATURE OF GHOST DISTRIBUTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 06 October 2022, pp. 374-389
- Print publication:
- June 2023
-
- Article
- Export citation
On the greatest common divisor of n and the nth Fibonacci number, II
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 06 October 2022, pp. 617-625
- Print publication:
- June 2023
-
- Article
- Export citation
ON LINEARISED POLYNOMIALS, SIDON ARRAYS AND FAST CONSTRUCTION OF SIDON SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 30 August 2022, pp. 376-384
- Print publication:
- December 2022
-
- Article
- Export citation
A new upper bound for sets with no square differences
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 30 September 2022, pp. 1777-1798
- Print publication:
- August 2022
-
- Article
- Export citation
A
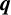 $\boldsymbol {q}$-SUPERCONGRUENCE MODULO THE THIRD POWER OF A CYCLOTOMIC POLYNOMIAL
$\boldsymbol {q}$-SUPERCONGRUENCE MODULO THE THIRD POWER OF A CYCLOTOMIC POLYNOMIAL
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 18 July 2022, pp. 236-242
- Print publication:
- October 2022
-
- Article
- Export citation
New lower bounds for van der Waerden numbers
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 13 July 2022, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A GENERALISATION OF A SUPERCONGRUENCE ON THE TRUNCATED APPELL SERIES
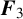 $\boldsymbol F_3$
$\boldsymbol F_3$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 13 July 2022, pp. 296-303
- Print publication:
- April 2023
-
- Article
- Export citation
BINARY SIGNED-DIGIT REPRESENTATIONS IN PAPERFOLDING
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 10 June 2022, pp. 363-375
- Print publication:
- December 2022
-
- Article
- Export citation
Joint ergodicity of fractional powers of primes
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 09 June 2022, e30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A SHARP UPPER BOUND FOR THE SUM OF RECIPROCALS OF LEAST COMMON MULTIPLES II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 09 June 2022, pp. 10-21
- Print publication:
- February 2023
-
- Article
- Export citation
A NEW
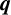 $\boldsymbol {q}$-ANALOGUE OF VAN HAMME’S (A.2) SUPERCONGRUENCE
$\boldsymbol {q}$-ANALOGUE OF VAN HAMME’S (A.2) SUPERCONGRUENCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 20 May 2022, pp. 22-30
- Print publication:
- February 2023
-
- Article
- Export citation
NEW GENERALISATIONS OF VAN HAMME’S (G.2) SUPERCONGRUENCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 18 May 2022, pp. 177-183
- Print publication:
- April 2023
-
- Article
- Export citation
Casting light on shadow Somos sequences
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue S1 / May 2023
- Published online by Cambridge University Press:
- 10 May 2022, pp. S87-S101
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ALTERNATING CIRCULAR SUMS OF BINOMIAL COEFFICIENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 13 April 2022, pp. 385-395
- Print publication:
- December 2022
-
- Article
- Export citation
Terms of Lucas sequences having a large smooth divisor
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 25 March 2022, pp. 225-231
- Print publication:
- March 2023
-
- Article
- Export citation
Combinatorial and harmonic-analytic methods for integer tilings
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 09 March 2022, e8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE DIVISOR FUNCTION OVER NONHOMOGENEOUS BEATTY SEQUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 04 March 2022, pp. 280-287
- Print publication:
- October 2022
-
- Article
- Export citation