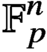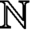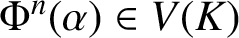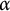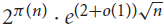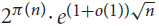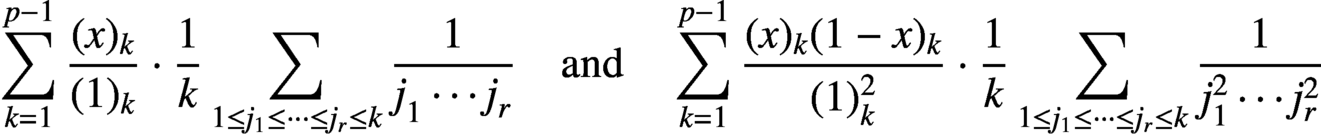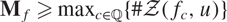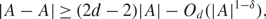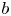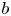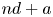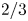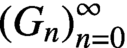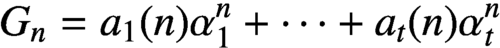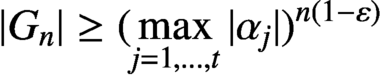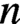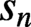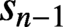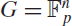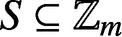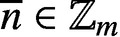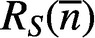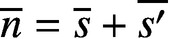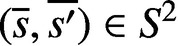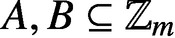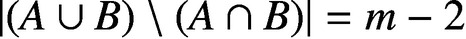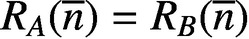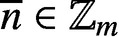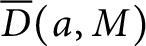Refine listing
Actions for selected content:
336 results in 11Bxx
High-entropy dual functions over finite fields and locally decodable codes
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 08 March 2021, e19
-
- Article
-
- You have access
- Open access
- Export citation
Sumsets of semiconvex sets
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 26 February 2021, pp. 84-94
- Print publication:
- March 2022
-
- Article
- Export citation
A SPARSITY RESULT FOR THE DYNAMICAL MORDELL–LANG CONJECTURE IN POSITIVE CHARACTERISTIC
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 23 February 2021, pp. 381-390
- Print publication:
- December 2021
-
- Article
- Export citation
On the Skolem problem and some related questions for parametric families of linear recurrence sequences
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 08 February 2021, pp. 773-792
- Print publication:
- June 2022
-
- Article
- Export citation
A variant of the Corners theorem
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 3 / November 2021
- Published online by Cambridge University Press:
- 02 February 2021, pp. 607-621
- Print publication:
- November 2021
-
- Article
- Export citation
The number of maximum primitive sets of integers
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 30 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 28 January 2021, pp. 781-795
-
- Article
- Export citation
TWO SUPERCONGRUENCES RELATED TO MULTIPLE HARMONIC SUMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 28 January 2021, pp. 379-389
- Print publication:
- June 2021
-
- Article
- Export citation
Primitive prime divisors in the critical orbits of one-parameter families of rational polynomials
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 3 / November 2021
- Published online by Cambridge University Press:
- 25 January 2021, pp. 569-584
- Print publication:
- November 2021
-
- Article
- Export citation
Boxes, extended boxes and sets of positive upper density in the Euclidean space
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 3 / November 2021
- Published online by Cambridge University Press:
- 14 January 2021, pp. 481-501
- Print publication:
- November 2021
-
- Article
-
- You have access
- Open access
- Export citation
ON A FABRIC OF KISSING CIRCLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 08 January 2021, pp. 320-329
- Print publication:
- October 2021
-
- Article
- Export citation
Bounds for sets with no polynomial progressions
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 05 January 2021, e16
-
- Article
-
- You have access
- Open access
- Export citation
Difference sets in higher dimensions
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 3 / November 2021
- Published online by Cambridge University Press:
- 14 December 2020, pp. 467-480
- Print publication:
- November 2021
-
- Article
- Export citation
The level of distribution of the Thue–Morse sequence
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 25 January 2021, pp. 2560-2587
- Print publication:
- December 2020
-
- Article
- Export citation
On the prime factors of the iterates of the Ramanujan τ–function
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 11 November 2020, pp. 1031-1047
-
- Article
- Export citation
ON THE GROWTH OF LINEAR RECURRENCES IN FUNCTION FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 09 November 2020, pp. 11-20
- Print publication:
- August 2021
-
- Article
-
- You have access
- Open access
- Export citation
EXPONENTIAL SUMS AND ADDITIVE COMBINATORICS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 09 November 2020, pp. 506-508
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation
LOOK, KNAVE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 21 October 2020, pp. 210-217
- Print publication:
- April 2021
-
- Article
- Export citation
Popular differences for corners in Abelian groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 1 / July 2021
- Published online by Cambridge University Press:
- 07 October 2020, pp. 207-225
- Print publication:
- July 2021
-
- Article
- Export citation
PARTITIONS OF
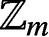 $\mathbb {Z}_m$ WITH IDENTICAL REPRESENTATION FUNCTION
$\mathbb {Z}_m$ WITH IDENTICAL REPRESENTATION FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 22 September 2020, pp. 204-209
- Print publication:
- April 2021
-
- Article
- Export citation
Dyson’s rank, overpartitions, and universal mock theta functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 07 September 2020, pp. 687-696
- Print publication:
- September 2021
-
- Article
- Export citation