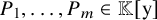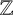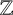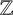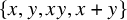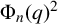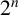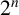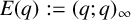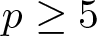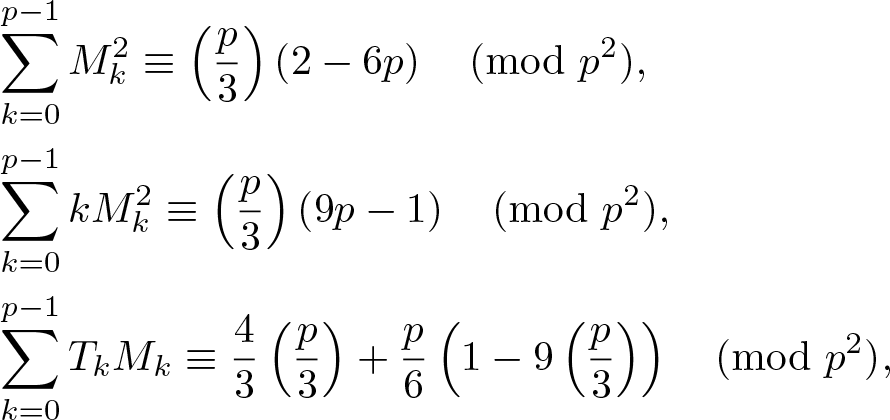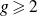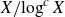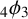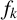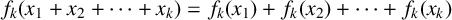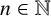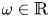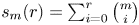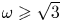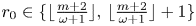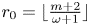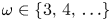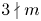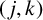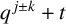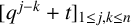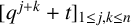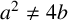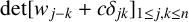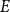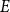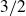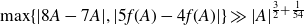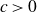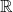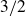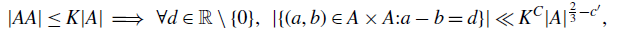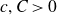Refine listing
Actions for selected content:
343 results in 11Bxx
Simplices in large sets and directional expansion in ergodic actions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 December 2024, e121
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Polynomial progressions in topological fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 26 November 2024, e106
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ADDITIVE AND SUBTRACTIVE BASES OF
 $\mathbb {Z}_m$ IN AVERAGE
$\mathbb {Z}_m$ IN AVERAGE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 47-56
- Print publication:
- August 2025
-
- Article
- Export citation
Arithmetic Ramsey theory over the primes
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 20 November 2024, pp. 1-47
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Product of polynomial values being large power
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 18 November 2024, pp. 51-62
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Intersective sets for sparse sets of integers
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 06 November 2024, pp. 1370-1402
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SPANNING TREES IN
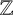 $\mathbb {Z}$-COVERS OF A FINITE GRAPH AND MAHLER MEASURES
$\mathbb {Z}$-COVERS OF A FINITE GRAPH AND MAHLER MEASURES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 28 October 2024, pp. 108-144
-
- Article
- Export citation
Monochromatic products and sums in the rationals
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 21 October 2024, e17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONGRUENCES FOR SUMS OF MACMAHON’S q-CATALAN POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 08 October 2024, pp. 416-427
- Print publication:
- June 2025
-
- Article
- Export citation
A PROOF OF HIRSCHHORN’S CONJECTURE ON
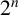 $2^n$-DISSECTION OF EULER’S PRODUCT
$2^n$-DISSECTION OF EULER’S PRODUCT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 08 October 2024, pp. 186-196
- Print publication:
- April 2025
-
- Article
- Export citation
THEOREM OF WARD ON SYMMETRIES OF ELLIPTIC NETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 04 October 2024, pp. 93-106
- Print publication:
- February 2025
-
- Article
- Export citation
Supercongruences involving Motzkin numbers and central trinomial coefficients
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 4 / November 2024
- Published online by Cambridge University Press:
- 03 October 2024, pp. 1060-1084
-
- Article
- Export citation
Most integers are not a sum of two palindromes
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 2 / September 2024
- Published online by Cambridge University Press:
- 22 October 2024, pp. 363-366
- Print publication:
- September 2024
-
- Article
- Export citation
A q-SUPERCONGRUENCE ARISING FROM ANDREWS’
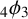 $_4\phi _3$ IDENTITY
$_4\phi _3$ IDENTITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 29 August 2024, pp. 223-227
- Print publication:
- April 2025
-
- Article
- Export citation
MULTIPLICATIVE FUNCTIONS k-ADDITIVE ON GENERALISED OCTAGONAL NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 27 August 2024, pp. 212-222
- Print publication:
- April 2025
-
- Article
- Export citation
Maximizing weighted sums of binomial coefficients using generalized continued fractions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 27 August 2024, pp. 1-16
-
- Article
- Export citation
CHARACTERISTIC POLYNOMIALS OF THE MATRICES WITH
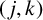 $(\,j,k)$-ENTRY
$(\,j,k)$-ENTRY 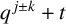 $q^{\,j\pm k}+t$
$q^{\,j\pm k}+t$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 03 June 2024, pp. 228-237
- Print publication:
- April 2025
-
- Article
- Export citation
A generalisation of Varnavides’s theorem
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 29 May 2024, pp. 724-728
-
- Article
- Export citation
A better than
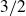 $3/2$ exponent for iterated sums and products over
$3/2$ exponent for iterated sums and products over 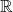 $\mathbb R$
$\mathbb R$
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 1 / July 2024
- Published online by Cambridge University Press:
- 10 May 2024, pp. 11-22
- Print publication:
- July 2024
-
- Article
- Export citation
A solution to the Erdős–Sárközy–Sós problem on asymptotic Sidon bases of order 3
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 10 May 2024, pp. 1418-1432
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation