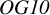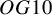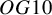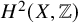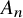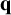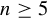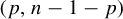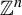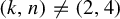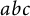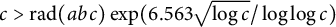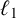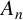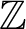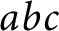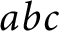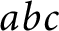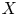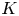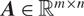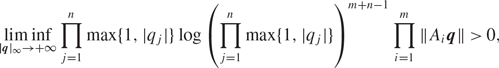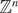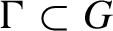Refine listing
Actions for selected content:
59 results in 11Hxx
VORONOI COMPLEXES IN HIGHER DIMENSIONS, COHOMOLOGY OF
 $GL_N(\mathbb{Z} )$ FOR
$GL_N(\mathbb{Z} )$ FOR  $N\geqslant 8$ AND THE TRIVIALITY OF
$N\geqslant 8$ AND THE TRIVIALITY OF  $K_8(\mathbb{Z} )$
$K_8(\mathbb{Z} )$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 24 November 2025, pp. 1-26
-
- Article
- Export citation
QUANTITATIVE GROWTH OF LINEAR RECURRENCES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 06 October 2025, pp. 1-34
-
- Article
- Export citation
Linearly exponential checking is enough for the lonely runner conjecture and some of its variants
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 01 October 2025, e164
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unimodular Hunting II
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 26 August 2025, e136
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finite groups of symplectic birational transformations of IHS manifolds of
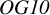 $\mathit {OG10}$ type
$\mathit {OG10}$ type
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 14 July 2025, e117
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Squarefree values of polynomial discriminants II
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 13 May 2025, e17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On elements of prescribed norm in maximal orders of a quaternion algebra
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 6 / December 2025
- Published online by Cambridge University Press:
- 11 November 2024, pp. 1938-1965
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic distribution for pairs of linear and quadratic forms at integral vectors
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 17 April 2024, pp. 111-139
- Print publication:
- January 2025
-
- Article
- Export citation
Equidistribution of rational subspaces and their shapes
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 10 November 2023, pp. 2009-2062
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A new lower bound in the
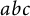 $abc$ conjecture
$abc$ conjecture
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 09 October 2023, pp. 369-378
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finite subgroups of automorphisms of K3 surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 27 June 2023, e54
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Enriques surfaces and an Apollonian packing in eight dimensions
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 11 July 2022, pp. 205-221
- Print publication:
- January 2023
-
- Article
- Export citation
Bounds for spectral projectors on tori
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 12 May 2022, e24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Reductions of abelian surfaces over global function fields
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 16 June 2022, pp. 893-950
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ABELIAN DIFFERENCE SETS AS LATTICE COVERINGS AND LATTICE TILINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 24 January 2022, pp. 177-184
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Arithmetic derivatives through geometry of numbers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 10 December 2021, pp. 906-923
- Print publication:
- December 2022
-
- Article
- Export citation
Successive minima and asymptotic slopes in Arakelov geometry
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 10 June 2021, pp. 1302-1339
- Print publication:
- June 2021
-
- Article
- Export citation
Multiplicatively badly approximable matrices up to logarithmic factors
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 17 May 2021, pp. 685-703
- Print publication:
- May 2022
-
- Article
- Export citation
Non-dense orbits on homogeneous spaces and applications to geometry and number theory
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 4 / April 2022
- Published online by Cambridge University Press:
- 18 March 2021, pp. 1327-1372
- Print publication:
- April 2022
-
- Article
- Export citation
Eigenfunctions of the Fourier transform with specified zeros
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 2 / September 2021
- Published online by Cambridge University Press:
- 15 February 2021, pp. 329-367
- Print publication:
- September 2021
-
- Article
- Export citation