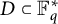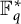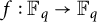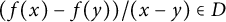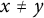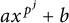Refine listing
Actions for selected content:
115 results in 11Txx
Equidistribution for nilsequences along spheres over finite fields
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 29 December 2025, pp. 1-73
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON SOME QUADRATICS AND CUBICS OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 28 November 2025, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on transverse sets and bilinear varieties
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 27 November 2025, pp. 1-13
-
- Article
- Export citation
Revisiting sums and products in countable and finite fields
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 13 October 2025, pp. 1-32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on twisted moments of Dirichlet
 $\boldsymbol{L}$-functions
$\boldsymbol{L}$-functions
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 24 September 2025, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Eigenvalue Method in coding theory
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 22 September 2025, pp. 1-41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE PRIMITIVITY OF THE TRINOMIAL
 $x^{n}+ax^{k}+b$ OVER
$x^{n}+ax^{k}+b$ OVER  $\mathbb {F}_{q}$
$\mathbb {F}_{q}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 11 September 2025, pp. 1-5
-
- Article
- Export citation
Moments of random multiplicative functions over function fields
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 3 / November 2025
- Published online by Cambridge University Press:
- 08 August 2025, pp. 785-819
- Print publication:
- November 2025
-
- Article
- Export citation
On a theorem of Mattila in the finite p-adic setting
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 14 July 2025, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Moments, Exponential Sums, and Monodromy Groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 26 June 2025, e101
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Iterating additive polynomials over finite fields
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 25 March 2025, pp. 795-810
-
- Article
- Export citation
A function field analog of Jacobi’s theorem on sums of squares and its moments
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 10 January 2025, pp. 667-683
- Print publication:
- September 2025
-
- Article
- Export citation
Bilinear Kloosterman sums in function fields and the distribution of irreducible polynomials
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 20 December 2024, pp. 1-26
-
- Article
- Export citation
A strengthening of McConnel’s theorem on permutations over finite fields
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 20 December 2024, pp. 213-218
- Print publication:
- March 2025
-
- Article
- Export citation
The Brun–Hooley sieve for 𝔽2[X] and squarefree shifts of integer polynomials
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 4 / November 2024
- Published online by Cambridge University Press:
- 06 November 2024, pp. 1171-1195
-
- Article
- Export citation
Smooth permutations and polynomials revisited
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 3 / November 2024
- Published online by Cambridge University Press:
- 11 December 2024, pp. 455-480
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON CONSECUTIVE RESIDUES AND NONRESIDUES UNDER A LINEAR MAP IN A FINITE FIELD
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 11 October 2024, pp. 505-512
- Print publication:
- June 2025
-
- Article
- Export citation
NONMONOGENITY OF NUMBER FIELDS DEFINED BY TRUNCATED EXPONENTIAL POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 08 October 2024, pp. 497-504
- Print publication:
- June 2025
-
- Article
- Export citation
A CONJECTURE OF ZHI-WEI SUN ON MATRICES CONCERNING MULTIPLICATIVE SUBGROUPS OF FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 27 September 2024, pp. 490-496
- Print publication:
- June 2025
-
- Article
- Export citation
Random walks and the “Euclidean” association scheme in finite vector spaces
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 24 May 2024, pp. 1664-1685
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation