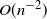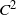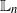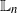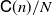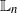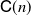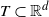Refine listing
Actions for selected content:
236 results in 65Cxx
On Markov chain approximations for computing boundary crossing probabilities of diffusion processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 11 May 2023, pp. 1386-1415
- Print publication:
- December 2023
-
- Article
- Export citation
Non-reversible guided Metropolis kernel
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 12 April 2023, pp. 955-981
- Print publication:
- September 2023
-
- Article
- Export citation
A new lifetime distribution by maximizing entropy: properties and applications
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 38 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 28 February 2023, pp. 189-206
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal scaling of MCMC beyond Metropolis
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 16 December 2022, pp. 492-509
- Print publication:
- June 2023
-
- Article
- Export citation
On mixed fractional stochastic differential equations with discontinuous drift coefficient
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 01 December 2022, pp. 589-606
- Print publication:
- June 2023
-
- Article
- Export citation
Matrix calculations for moments of Markov processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 55 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 02 September 2022, pp. 126-150
- Print publication:
- March 2023
-
- Article
- Export citation
Log-normalization constant estimation using the ensemble Kalman–Bucy filter with application to high-dimensional models
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 02 September 2022, pp. 1139-1163
- Print publication:
- December 2022
-
- Article
- Export citation
A note on the polynomial ergodicity of the one-dimensional Zig-Zag process
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 18 July 2022, pp. 895-903
- Print publication:
- September 2022
-
- Article
- Export citation
Unbiased filtering of a class of partially observed diffusions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 15 June 2022, pp. 661-687
- Print publication:
- September 2022
-
- Article
- Export citation
Optimal consumption with Hindy–Huang–Kreps preferences under nonlinear expectations
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 14 June 2022, pp. 1222-1251
- Print publication:
- December 2022
-
- Article
- Export citation
A systematic analysis of the memory term in coarse-grained models: The case of the Markovian approximation
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 08 June 2022, pp. 326-345
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Efficient simulation of coupled gas and power networks under uncertain demands
- Part of
- Partial differential equations, initial value and time-dependent initial-boundary value problems
- Compressible fluids and gas dynamics, general
- The Mathematics in Renewable Energy special issue
- Probabilistic methods, simulation and stochastic differential equations
- Operations research and management science
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 04 April 2022, pp. 505-531
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Exact simulation of extrinsic stress-release processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 14 February 2022, pp. 105-117
- Print publication:
- March 2022
-
- Article
- Export citation
Efficient conditional Monte Carlo simulations for the exponential integrals of Gaussian random fields
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 366-383
- Print publication:
- June 2022
-
- Article
- Export citation
An ergodic theorem for the weighted ensemble method
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 18 January 2022, pp. 152-166
- Print publication:
- March 2022
-
- Article
- Export citation
A note on the Screaming Toes game
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 17 January 2022, pp. 118-130
- Print publication:
- March 2022
-
- Article
- Export citation
Exact simulation of coupled Wright–Fisher diffusions
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 923-950
- Print publication:
- December 2021
-
- Article
- Export citation
Approximations of geometrically ergodic reversible markov chains
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 22 November 2021, pp. 981-1022
- Print publication:
- December 2021
-
- Article
- Export citation
WEIGHTED INTER-RATER AGREEMENT MEASURES FOR ORDINAL OUTCOMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 01 October 2021, pp. 173-174
- Print publication:
- February 2022
-
- Article
-
- You have access
- HTML
- Export citation
Diffusion approximation of multi-class Hawkes processes: Theoretical and numerical analysis
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 53 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 08 October 2021, pp. 716-756
- Print publication:
- September 2021
-
- Article
- Export citation