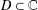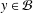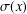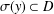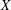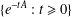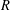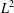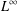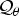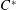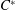Refine listing
Actions for selected content:
300 results in 47Axx
Shadowing and structural stability for operators
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 10 January 2020, pp. 961-980
- Print publication:
- April 2021
-
- Article
- Export citation
INEQUALITIES OF JENSEN’S TYPE FOR POSITIVE LINEAR FUNCTIONALS ON HERMITIAN UNITAL BANACH
 $\ast$-ALGEBRAS
$\ast$-ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 308-318
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
Frequent universality criterion and densities
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 25 November 2019, pp. 846-868
- Print publication:
- March 2021
-
- Article
- Export citation
Escaping a Neighborhood Along a Prescribed Sequence in Lie Groups and Banach Algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 02 October 2019, pp. 484-505
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
CONTINUITY OF A CONDITION SPECTRUM AND ITS LEVEL SETS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 09 September 2019, pp. 412-430
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
PACKING SUBORDINACY WITH APPLICATION TO SPECTRAL CONTINUITY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 13 June 2019, pp. 226-244
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
CONVEXITY OF PARAMETER EXTENSIONS OF SOME RELATIVE OPERATOR ENTROPIES WITH A PERSPECTIVE APPROACH
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 06 June 2019, pp. 737-744
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
Simultaneous Upper Triangular Forms for Commuting Operators in a Finite von Neumann Algebra
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 15 May 2019, pp. 1188-1245
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
LIPSCHITZ-TYPE INEQUALITIES FOR ANALYTIC FUNCTIONS IN BANACH ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 11 April 2019, pp. 489-497
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
NEW COUNTEREXAMPLES ON RITT OPERATORS, SECTORIAL OPERATORS AND
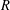 $R$-BOUNDEDNESS
$R$-BOUNDEDNESS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 11 April 2019, pp. 498-506
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
Biholomorphic Mappings on Banach Spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 4 / November 2019
- Published online by Cambridge University Press:
- 27 February 2019, pp. 913-924
-
- Article
- Export citation
RECOVERY OF THE TEMPERATURE DISTRIBUTION IN A MULTILAYER FRACTIONAL DIFFUSION EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 20 February 2019, pp. 344-352
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
On quotient modules of H2(𝔻n): essential normality and boundary representations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 31 January 2019, pp. 1339-1359
- Print publication:
- June 2020
-
- Article
- Export citation
On a second numerical index for Banach spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 28 January 2019, pp. 1003-1051
- Print publication:
- April 2020
-
- Article
- Export citation
Optimal growth of harmonic functions frequently hypercyclic for the partial differentiation operator
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 18 January 2019, pp. 1577-1594
- Print publication:
- December 2019
-
- Article
- Export citation
Some generic properties of Schrödinger operators with radial potentials
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 15 January 2019, pp. 1435-1451
- Print publication:
- December 2019
-
- Article
- Export citation
Elements of
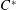 $C^{\ast }$-algebras Attaining their Norm in a Finite-dimensional Representation
$C^{\ast }$-algebras Attaining their Norm in a Finite-dimensional Representation
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 93-111
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
Linear Maps Preserving Matrices of Local Spectral Radius Zero at a Fixed Vector
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 749-771
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
ON THE DECOMPOSITION OF OPERATORS WITH SEVERAL ALMOST-INVARIANT SUBSPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 04 January 2019, pp. 274-283
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
Determinant of the Laplacian on Tori of Constant Positive Curvature with one Conical Point
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 04 January 2019, pp. 341-347
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation