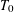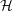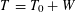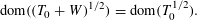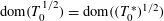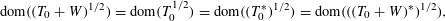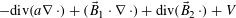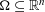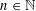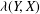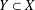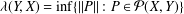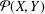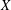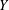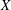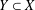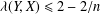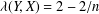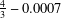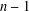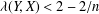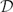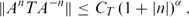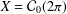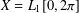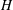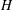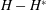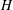Refine listing
Actions for selected content:
300 results in 47Axx
POLISH MODELS AND SOFIC ENTROPY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 18 January 2016, pp. 241-275
- Print publication:
- April 2018
-
- Article
- Export citation
On functional calculus properties of Ritt operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 6 / December 2015
- Published online by Cambridge University Press:
- 26 November 2015, pp. 1239-1250
- Print publication:
- December 2015
-
- Article
- Export citation
High Order Finite Difference Discretization for Composite Grid Hierarchy and Its Applications
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 18 / Issue 5 / November 2015
- Published online by Cambridge University Press:
- 23 November 2015, pp. 1211-1233
- Print publication:
- November 2015
-
- Article
- Export citation
SPECTRUM AND COMPACTNESS OF THE CESÀRO OPERATOR ON WEIGHTED
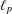 $\ell _{p}$ SPACES
$\ell _{p}$ SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 19 August 2015, pp. 287-314
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
STABILITY OF UNCONDITIONAL SCHAUDER DECOMPOSITIONS IN
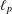 $\ell _{p}$ SPACES
$\ell _{p}$ SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 03 August 2015, pp. 444-456
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
EMBEDDING AND TRACE RESULTS FOR VARIABLE EXPONENT SOBOLEV AND MAZ'YA SPACES ON NON-SMOOTH DOMAINS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 471-489
- Print publication:
- May 2016
-
- Article
-
- You have access
- Export citation
LEBESGUE DECOMPOSITION FOR REPRESENTABLE FUNCTIONALS ON *-ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 58 / Issue 2 / May 2016
- Published online by Cambridge University Press:
- 21 July 2015, pp. 491-501
- Print publication:
- May 2016
-
- Article
-
- You have access
- Export citation
Boundedness of integral operators on decreasing functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 4 / August 2015
- Published online by Cambridge University Press:
- 30 June 2015, pp. 725-744
- Print publication:
- August 2015
-
- Article
- Export citation
LEVEL SETS OF THE RESOLVENT NORM OF A LINEAR OPERATOR REVISITED
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 26 June 2015, pp. 243-265
- Print publication:
- 2016
-
- Article
- Export citation
ON STABILITY OF SQUARE ROOT DOMAINS FOR NON-SELF-ADJOINT OPERATORS UNDER ADDITIVE PERTURBATIONS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 12 March 2015, pp. 111-182
- Print publication:
- 2016
-
- Article
- Export citation
HYPERPLANES OF FINITE-DIMENSIONAL NORMED SPACES WITH THE MAXIMAL RELATIVE PROJECTION CONSTANT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 02 March 2015, pp. 447-463
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
Eigentime Identity for One-Dimensional Diffusion Processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 52 / Issue 1 / March 2015
- Published online by Cambridge University Press:
- 30 January 2018, pp. 224-237
- Print publication:
- March 2015
-
- Article
-
- You have access
- Export citation
ON COSINE FAMILIES CLOSE TO SCALAR COSINE FAMILIES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 26 February 2015, pp. 166-174
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
ISOSPECTRALITY FOR GRAPH LAPLACIANS UNDER THE CHANGE OF COUPLING AT GRAPH VERTICES: NECESSARY AND SUFFICIENT CONDITIONS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 16 January 2015, pp. 210-242
- Print publication:
- 2016
-
- Article
- Export citation
GROWTH CONDITIONS FOR OPERATORS WITH SMALLEST SPECTRUM
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 18 December 2014, pp. 665-680
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
MAPS PRESERVING THE LOCAL SPECTRUM OF PRODUCT OF OPERATORS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 17 December 2014, pp. 709-718
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
THE BEST WEIGHTED GRADIENT APPROXIMATION TO AN OBSERVED FUNCTION
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 14 October 2014, pp. 54-68
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
ON THE MINIMAL PROPERTY OF DE LA VALLÉE POUSSIN’S OPERATOR
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 08 October 2014, pp. 129-133
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
A BOUND FOR SIMILARITY CONDITION NUMBERS OF UNBOUNDED OPERATORS WITH HILBERT–SCHMIDT HERMITIAN COMPONENTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 12 September 2014, pp. 331-342
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
SOME INEQUALITIES OF JENSEN TYPE FOR ARG-SQUARE CONVEX FUNCTIONS OF UNITARY OPERATORS IN HILBERT SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 12 May 2014, pp. 65-73
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
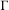
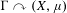
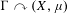
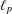
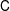
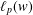
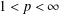
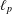

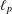
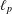
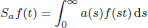
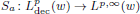 was completely solved, the characterization of the weights
was completely solved, the characterization of the weights 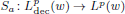 is bounded is still open for the case in which
is bounded is still open for the case in which