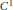Refine listing
Actions for selected content:
300 results in 47Axx
STRUCTURE THEOREM FOR
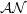 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathcal{AN}$-OPERATORS
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathcal{AN}$-OPERATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 30 April 2014, pp. 386-395
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
REFLEXIVE INDEX OF A FAMILY OF SUBSPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 1 / August 2014
- Published online by Cambridge University Press:
- 02 April 2014, pp. 134-140
- Print publication:
- August 2014
-
- Article
-
- You have access
- Export citation
ON SMALL SUBSPACE LATTICES IN HILBERT SPACE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 96 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 15 October 2013, pp. 44-60
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
THE SIMILARITY DEGREE OF SOME
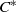 ${C}^{\ast } $-ALGEBRAS
${C}^{\ast } $-ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 1 / February 2014
- Published online by Cambridge University Press:
- 27 June 2013, pp. 60-69
- Print publication:
- February 2014
-
- Article
-
- You have access
- Export citation
GROUPOID
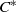 ${C}^{\ast } $-ALGEBRAS WITH HAUSDORFF SPECTRUM
${C}^{\ast } $-ALGEBRAS WITH HAUSDORFF SPECTRUM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 08 March 2013, pp. 232-242
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
TRACE INEQUALITIES AND A QUESTION OF BOURIN
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 25 January 2013, pp. 384-389
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
BOUNDARY ANGULAR DERIVATIVES OF GENERALIZED SCHUR FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 08 March 2013, pp. 203-224
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
Improved local energy decay for the wave equation on asymptotically Euclidean odd dimensional manifolds in the short range case
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 12 / Issue 3 / July 2013
- Published online by Cambridge University Press:
- 13 July 2012, pp. 635-650
- Print publication:
- July 2013
-
- Article
- Export citation
REPRESENTATION THEOREMS FOR INDEFINITE QUADRATIC FORMS REVISITED
- Part of
-
- Journal:
- Mathematika / Volume 59 / Issue 1 / January 2013
- Published online by Cambridge University Press:
- 12 June 2012, pp. 169-189
- Print publication:
- January 2013
-
- Article
- Export citation
Cyclicity of singular inner functions from the corona theorem
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 11 / Issue 4 / October 2012
- Published online by Cambridge University Press:
- 31 May 2012, pp. 815-824
- Print publication:
- October 2012
-
- Article
- Export citation
SPECTRAL STABILITY ESTIMATES FOR ELLIPTIC OPERATORS SUBJECT TO DOMAIN TRANSFORMATIONS WITH NON-UNIFORMLY BOUNDED GRADIENTS
- Part of
-
- Journal:
- Mathematika / Volume 58 / Issue 2 / July 2012
- Published online by Cambridge University Press:
- 24 February 2012, pp. 324-348
- Print publication:
- July 2012
-
- Article
- Export citation
SMALL ESSENTIAL SPECTRAL RADIUS PERTURBATIONS OF OPERATORS WITH TOPOLOGICAL UNIFORM DESCENT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 85 / Issue 1 / February 2012
- Published online by Cambridge University Press:
- 30 August 2011, pp. 26-45
- Print publication:
- February 2012
-
- Article
-
- You have access
- Export citation
Hypercyclic and mixing operator semigroups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 3 / October 2011
- Published online by Cambridge University Press:
- 27 June 2011, pp. 761-782
-
- Article
-
- You have access
- Export citation
ALGEBRAIC ASPECTS OF SPECTRAL THEORY
- Part of
-
- Journal:
- Mathematika / Volume 57 / Issue 1 / January 2011
- Published online by Cambridge University Press:
- 21 December 2010, pp. 63-88
- Print publication:
- January 2011
-
- Article
- Export citation
ON THE ISOPERIMETRIC PROBLEM FOR THE LAPLACIAN WITH ROBIN AND WENTZELL BOUNDARY CONDITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 2 / October 2010
- Published online by Cambridge University Press:
- 16 August 2010, pp. 348-350
- Print publication:
- October 2010
-
- Article
-
- You have access
- Export citation
ENDPOINT ESTIMATES FOR COMMUTATORS OF RIESZ TRANSFORMS ASSOCIATED WITH SCHRÖDINGER OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 82 / Issue 3 / December 2010
- Published online by Cambridge University Press:
- 16 August 2010, pp. 367-389
- Print publication:
- December 2010
-
- Article
-
- You have access
- Export citation
SPECTRAL RADIUS ALGEBRAS AND C0 CONTRACTIONS. II
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 89 / Issue 1 / August 2010
- Published online by Cambridge University Press:
- 22 September 2010, pp. 91-104
- Print publication:
- August 2010
-
- Article
-
- You have access
- Export citation
ITERATED LAVRENTIEV REGULARIZATION FOR NONLINEAR ILL-POSED PROBLEMS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 51 / Issue 2 / October 2009
- Published online by Cambridge University Press:
- 19 April 2010, pp. 191-217
-
- Article
-
- You have access
- Export citation
TENSOR EXTENSION PROPERTIES OF C(K)-REPRESENTATIONS AND APPLICATIONS TO UNCONDITIONALITY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 88 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 11 March 2010, pp. 205-230
- Print publication:
- April 2010
-
- Article
-
- You have access
- Export citation
Some Applications of the Perturbation Determinant in Finite von Neumann Algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 1 / 01 February 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 133-156
- Print publication:
- 01 February 2010
-
- Article
-
- You have access
- Export citation
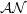
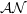
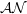

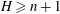
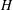

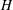
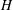

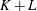
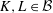
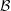

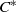
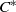
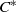
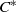
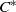
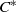
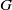
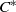
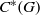
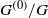
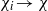
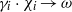
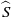
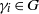
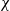
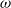
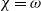
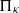
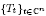 with holomorphic dependence on the parameter
with holomorphic dependence on the parameter 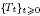 .
.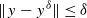 resulting in the convergence of the method as
resulting in the convergence of the method as