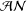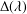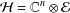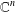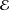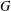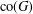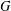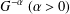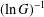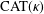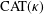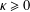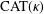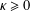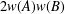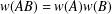Refine listing
Actions for selected content:
300 results in 47Axx
A NOTE ON POSITIVE
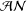 ${\mathcal{A}}{\mathcal{N}}$ OPERATORS
${\mathcal{A}}{\mathcal{N}}$ OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 26 December 2018, pp. 129-130
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
INVERSION OF OPERATOR PENCILS ON HILBERT SPACE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 21 December 2018, pp. 145-176
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
Chaotic backward shift operator on Chebyshev polynomials
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 30 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 21 December 2018, pp. 1025-1037
-
- Article
- Export citation
MULTIPLICITIES OF EIGENVALUES OF THE DIFFUSION OPERATOR WITH RANDOM JUMPS FROM THE BOUNDARY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 28 November 2018, pp. 101-113
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
An Inverse Result of Approximation by Sampling Kantorovich Series
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 16 October 2018, pp. 265-280
-
- Article
- Export citation
Well-posedness of Third Order Differential Equations in Hölder Continuous Function Spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 4 / December 2019
- Published online by Cambridge University Press:
- 15 October 2018, pp. 715-726
- Print publication:
- December 2019
-
- Article
-
- You have access
- Export citation
r-FREDHOLM THEORY IN BANACH ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 3 / September 2019
- Published online by Cambridge University Press:
- 25 September 2018, pp. 615-627
- Print publication:
- September 2019
-
- Article
-
- You have access
- Export citation
Arlinskii's Iteration and its Applications
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 29 August 2018, pp. 125-133
-
- Article
- Export citation
ORTHOGONALITY AND PARALLELISM OF OPERATORS ON VARIOUS BANACH SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 106 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 22 August 2018, pp. 160-183
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
A STRUCTURED INVERSE SPECTRUM PROBLEM FOR INFINITE GRAPHS ANDUNBOUNDED OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 3 / December 2018
- Published online by Cambridge University Press:
- 15 August 2018, pp. 363-371
- Print publication:
- December 2018
-
- Article
-
- You have access
- Export citation
A Trace Formula for the Index of B-Fredholm Operators
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 4 / November 2018
- Published online by Cambridge University Press:
- 06 August 2018, pp. 1063-1068
-
- Article
- Export citation
Andô dilations and inequalities on non-commutative domains
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 6 / December 2018
- Published online by Cambridge University Press:
- 06 July 2018, pp. 1239-1267
- Print publication:
- December 2018
-
- Article
- Export citation
FREQUENTLY HYPERCYCLIC BILATERAL SHIFTS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 20 June 2018, pp. 271-286
- Print publication:
- May 2019
-
- Article
-
- You have access
- Export citation
SIMILARITY OF OPERATORS ON TENSOR PRODUCTS OF SPACES AND MATRIX DIFFERENTIAL OPERATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 106 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 30 May 2018, pp. 19-30
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
CONVERGENCE OF MANN’S ALTERNATING PROJECTIONS IN CAT(
 $\unicode[STIX]{x1D705}$ ) SPACES
$\unicode[STIX]{x1D705}$ ) SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 03 May 2018, pp. 134-143
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
Note on Spectra of Non-Selfadjoint Operators Over Dynamical Systems
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 15 February 2018, pp. 371-386
-
- Article
- Export citation
IMPROVED INEQUALITIES FOR THE NUMERICAL RADIUS: WHEN INVERSE COMMUTES WITH THE NORM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 02 February 2018, pp. 293-296
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
Linear Surjective Maps Preserving at Least One Element from the Local Spectrum
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 23 January 2018, pp. 169-175
-
- Article
- Export citation
ALMOST INVARIANT HALF-SPACES FOR OPERATORS ON HILBERT SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 31 August 2017, pp. 133-140
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
Discreteness of spectrum for Schrödinger operators with δʹ-type conditions on infinite regular trees
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 5 / October 2017
- Published online by Cambridge University Press:
- 14 August 2017, pp. 1091-1117
- Print publication:
- October 2017
-
- Article
- Export citation