Refine listing
Actions for selected content:
300 results in 47Axx
Boundedness of rough singular integral operators on homogeneous Herz spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 66 / Issue 2 / April 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 201-223
- Print publication:
- April 1999
-
- Article
-
- You have access
- Export citation
Subordination in the sense of Bochner and a related functional calculus
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 3 / June 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 368-396
- Print publication:
- June 1998
-
- Article
-
- You have access
- Export citation
Ergodicity and differences of functions on semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 2 / April 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 253-265
- Print publication:
- April 1998
-
- Article
-
- You have access
- Export citation
Modified cauchy kernels and functional calculus for operators on Banach space
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 63 / Issue 1 / August 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 91-99
- Print publication:
- August 1997
-
- Article
-
- You have access
- Export citation
Spectral and asymptotic properties of dominated operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 63 / Issue 1 / August 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 16-31
- Print publication:
- August 1997
-
- Article
-
- You have access
- Export citation
Banach space operators with a bounded H∞ functional calculus
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 1 / February 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 51-89
- Print publication:
- February 1996
-
- Article
-
- You have access
- Export citation
Some trace inequalities for operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 58 / Issue 2 / April 1995
- Published online by Cambridge University Press:
- 09 April 2009, pp. 281-286
- Print publication:
- April 1995
-
- Article
-
- You have access
- Export citation
Approximations of positive operators and continuity of the spectral radius III
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 57 / Issue 3 / December 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 330-340
- Print publication:
- December 1994
-
- Article
-
- You have access
- Export citation
Invariant subspaces in the bidisc and commutators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 56 / Issue 2 / April 1994
- Published online by Cambridge University Press:
- 09 April 2009, pp. 232-242
- Print publication:
- April 1994
-
- Article
-
- You have access
- Export citation
Generation of generators of holomorphic semigroups
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 55 / Issue 2 / October 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 246-269
- Print publication:
- October 1993
-
- Article
-
- You have access
- Export citation
The spectral theorem for well-bounded operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 54 / Issue 3 / June 1993
- Published online by Cambridge University Press:
- 09 April 2009, pp. 334-351
- Print publication:
- June 1993
-
- Article
-
- You have access
- Export citation
On strongly stable approximations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 52 / Issue 2 / April 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 251-260
- Print publication:
- April 1992
-
- Article
-
- You have access
- Export citation
The spectra of weighted mean operators on bν0
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 52 / Issue 2 / April 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 242-250
- Print publication:
- April 1992
-
- Article
-
- You have access
- Export citation
Hyponormal operators on uniformly smooth spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 1 / February 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 150-159
- Print publication:
- February 1991
-
- Article
-
- You have access
- Export citation
Operator approximations with stable elgenvalues
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 2 / October 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 250-257
- Print publication:
- October 1990
-
- Article
-
- You have access
- Export citation
Eigenelements of perturbed operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 1 / August 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 138-148
- Print publication:
- August 1990
-
- Article
-
- You have access
- Export citation
On the spectrum of C1 as an operator on bv0
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 48 / Issue 1 / February 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 79-86
- Print publication:
- February 1990
-
- Article
-
- You have access
- Export citation
H∞ functional calculus of elliptic operators with C∞ coefficients on Lp spaces of smooth domains
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 48 / Issue 1 / February 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 113-123
- Print publication:
- February 1990
-
- Article
-
- You have access
- Export citation
The non-emptiness of joint spectral subsets of euclidean n-space
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 2 / October 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 300-306
- Print publication:
- October 1989
-
- Article
-
- You have access
- Export citation
On the Pták homomorphism theorem
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 2 / October 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 322-333
- Print publication:
- October 1989
-
- Article
-
- You have access
- Export citation
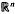 ) functions and Ricci-Stein oscillatory singular integral operators. Some new results are obtained.
) functions and Ricci-Stein oscillatory singular integral operators. Some new results are obtained.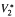 , For example, M is studied when the commutator is self-adjoint or of finite rank.
, For example, M is studied when the commutator is self-adjoint or of finite rank.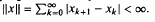 .
.