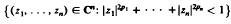Refine listing
Actions for selected content:
321 results in 47Bxx
On unilateral shift operators and C0-operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 53 / Issue 1 / August 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 137-142
- Print publication:
- August 1992
-
- Article
-
- You have access
- Export citation
On strongly stable approximations
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 52 / Issue 2 / April 1992
- Published online by Cambridge University Press:
- 09 April 2009, pp. 251-260
- Print publication:
- April 1992
-
- Article
-
- You have access
- Export citation
Multiplication operators on weighted spaces of vector-valued continuous functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 1 / February 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 98-107
- Print publication:
- February 1991
-
- Article
-
- You have access
- Export citation
The symmetric algebra of quotients of an ultraprime Banach algebra
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 50 / Issue 1 / February 1991
- Published online by Cambridge University Press:
- 09 April 2009, pp. 75-87
- Print publication:
- February 1991
-
- Article
-
- You have access
- Export citation
Operator approximations with stable elgenvalues
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 2 / October 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 250-257
- Print publication:
- October 1990
-
- Article
-
- You have access
- Export citation
Spectrality of elementary operators
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 49 / Issue 2 / October 1990
- Published online by Cambridge University Press:
- 09 April 2009, pp. 327-346
- Print publication:
- October 1990
-
- Article
-
- You have access
- Export citation
Invariant Vectors of a Nonrecurrent Markov Matrix
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 32 / Issue 3 / 01 September 1989
- Published online by Cambridge University Press:
- 20 November 2018, pp. 352-359
- Print publication:
- 01 September 1989
-
- Article
-
- You have access
- Export citation
Archimedes integrals and conuclear spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 1 / August 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 22-31
- Print publication:
- August 1989
-
- Article
-
- You have access
- Export citation
Positive semigroups of operators on Banach spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 47 / Issue 1 / August 1989
- Published online by Cambridge University Press:
- 09 April 2009, pp. 90-94
- Print publication:
- August 1989
-
- Article
-
- You have access
- Export citation
Composition operators on weighted spaces of continuous functions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 45 / Issue 3 / December 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 303-319
- Print publication:
- December 1988
-
- Article
-
- You have access
- Export citation
Scalar operators and integration
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 45 / Issue 3 / December 1988
- Published online by Cambridge University Press:
- 09 April 2009, pp. 401-420
- Print publication:
- December 1988
-
- Article
-
- You have access
- Export citation
Cp-classes of operators in C*-algebras
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 40 / Issue 2 / April 1986
- Published online by Cambridge University Press:
- 09 April 2009, pp. 153-160
- Print publication:
- April 1986
-
- Article
-
- You have access
- Export citation
The standard summation operator, the Euler-Maclaurin sum formula, and the Laplace transformation
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 39 / Issue 3 / December 1985
- Published online by Cambridge University Press:
- 09 April 2009, pp. 367-390
- Print publication:
- December 1985
-
- Article
-
- You have access
- Export citation
The Euler-Maclaurin sum formula for a closed derivation
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 37 / Issue 1 / August 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 128-138
- Print publication:
- August 1984
-
- Article
-
- You have access
- Export citation
On numerical ranges of generalized derivations and related properties
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 36 / Issue 1 / February 1984
- Published online by Cambridge University Press:
- 09 April 2009, pp. 134-142
- Print publication:
- February 1984
-
- Article
-
- You have access
- Export citation
A Joint spectral theorem for unbounded normal opertors
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 34 / Issue 2 / April 1983
- Published online by Cambridge University Press:
- 09 April 2009, pp. 203-213
- Print publication:
- April 1983
-
- Article
-
- You have access
- Export citation
A simple test for nuclearity of integral operators on L2(Rn)
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 33 / Issue 2 / October 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 193-196
- Print publication:
- October 1982
-
- Article
-
- You have access
- Export citation
Invariant subspace lattices of Lambert's weighted shifts
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 33 / Issue 1 / August 1982
- Published online by Cambridge University Press:
- 09 April 2009, pp. 135-142
- Print publication:
- August 1982
-
- Article
-
- You have access
- Export citation
Toeplitz operators on certain weakly pseudoconvex domains
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 31 / Issue 1 / June 1981
- Published online by Cambridge University Press:
- 09 April 2009, pp. 1-14
- Print publication:
- June 1981
-
- Article
-
- You have access
- Export citation
Weighted shifts and commuting normal extension
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 27 / Issue 1 / February 1979
- Published online by Cambridge University Press:
- 09 April 2009, pp. 17-26
- Print publication:
- February 1979
-
- Article
-
- You have access
- Export citation
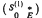 relative to a decomposition ℳ ⊕
relative to a decomposition ℳ ⊕ 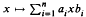 , acting on the algebra
, acting on the algebra 
 –semigroups is also given.
–semigroups is also given.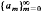 be a bounded sequence of positive real numbers. For a given injective operator
be a bounded sequence of positive real numbers. For a given injective operator 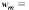
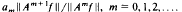 We define a weighted shift
We define a weighted shift 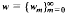 on the Hilbert space 1
on the Hilbert space 1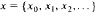 by
by 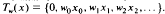 . The main object of this paper is to characterize the invariant subspace lattice of
. The main object of this paper is to characterize the invariant subspace lattice of 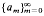 .
.