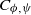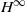Refine listing
Actions for selected content:
321 results in 47Bxx
BOUNDED TOEPLITZ AND HANKEL PRODUCTS ON THE WEIGHTED BERGMAN SPACES OF THE UNIT BALL
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 99 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 05 June 2015, pp. 237-249
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
TOEPLITZ OPERATORS BETWEEN FOCK SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 2 / October 2015
- Published online by Cambridge University Press:
- 02 June 2015, pp. 316-324
- Print publication:
- October 2015
-
- Article
-
- You have access
- Export citation
ON STABILITY OF SQUARE ROOT DOMAINS FOR NON-SELF-ADJOINT OPERATORS UNDER ADDITIVE PERTURBATIONS
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 12 March 2015, pp. 111-182
- Print publication:
- 2016
-
- Article
- Export citation
WEIGHTED COMPOSITION OPERATORS ON H∞ ∩
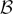 $\mathcal{B}$o
$\mathcal{B}$o
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 2 / May 2015
- Published online by Cambridge University Press:
- 17 December 2014, pp. 475-480
- Print publication:
- May 2015
-
- Article
-
- You have access
- Export citation
MAPS PRESERVING THE LOCAL SPECTRUM OF PRODUCT OF OPERATORS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 17 December 2014, pp. 709-718
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
Generalized Morrey Regularity for Parabolic Equations with Discontinuous Data
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 10 December 2014, pp. 199-218
-
- Article
-
- You have access
- Export citation
Spectral Analysis of Markov Kernels and Application to the Convergence Rate Of Discrete Random Walks
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 46 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 22 February 2016, pp. 1036-1058
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
On Nonlinear Boundary Conditions Involving Decomposable Linear Functionals
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 58 / Issue 2 / June 2015
- Published online by Cambridge University Press:
- 27 October 2014, pp. 421-439
-
- Article
-
- You have access
- Export citation
A BOUND FOR SIMILARITY CONDITION NUMBERS OF UNBOUNDED OPERATORS WITH HILBERT–SCHMIDT HERMITIAN COMPONENTS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 97 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 12 September 2014, pp. 331-342
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
DEPENDENCE OF EIGENVALUES OF SIXTH-ORDER BOUNDARY VALUE PROBLEMS ON THE BOUNDARY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 09 September 2014, pp. 457-468
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
A VARIATION ON SELBERG’S APPROXIMATION PROBLEM
- Part of
-
- Journal:
- Mathematika / Volume 61 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 14 August 2014, pp. 213-235
- Print publication:
- January 2015
-
- Article
- Export citation
QUASIHOMOGENEOUS TOEPLITZ OPERATORS WITH INTEGRABLE SYMBOLS ON THE HARMONIC BERGMAN SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 3 / December 2014
- Published online by Cambridge University Press:
- 13 June 2014, pp. 494-503
- Print publication:
- December 2014
-
- Article
-
- You have access
- Export citation
DOMINATION BY POSITIVE WEAK
 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}^{*}$ DUNFORD–PETTIS OPERATORS ON BANACH LATTICES
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}^{*}$ DUNFORD–PETTIS OPERATORS ON BANACH LATTICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 90 / Issue 2 / October 2014
- Published online by Cambridge University Press:
- 05 June 2014, pp. 311-318
- Print publication:
- October 2014
-
- Article
-
- You have access
- Export citation
THE FINITE SECTION METHOD FOR DISSIPATIVE OPERATORS
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 2 / July 2014
- Published online by Cambridge University Press:
- 14 May 2014, pp. 415-443
- Print publication:
- July 2014
-
- Article
- Export citation
BACKWARD 3-STEP EXTENSIONS OF RECURSIVELY GENERATED WEIGHTED SHIFTS: A RANGE OF QUADRATIC HYPONORMALITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 89 / Issue 3 / June 2014
- Published online by Cambridge University Press:
- 20 November 2013, pp. 488-493
- Print publication:
- June 2014
-
- Article
-
- You have access
- Export citation
Inverse spectral problems for compact Hankel operators
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 2 / April 2014
- Published online by Cambridge University Press:
- 18 April 2013, pp. 273-301
- Print publication:
- April 2014
-
- Article
- Export citation
On derivations and elementary operators on C*-algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 56 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 21 March 2013, pp. 515-534
-
- Article
-
- You have access
- Export citation
Regular Perturbation of V-Geometrically Ergodic Markov Chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 50 / Issue 1 / March 2013
- Published online by Cambridge University Press:
- 30 January 2018, pp. 184-194
- Print publication:
- March 2013
-
- Article
-
- You have access
- Export citation
TRACE INEQUALITIES AND A QUESTION OF BOURIN
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 3 / December 2013
- Published online by Cambridge University Press:
- 25 January 2013, pp. 384-389
- Print publication:
- December 2013
-
- Article
-
- You have access
- Export citation
ORDER BOUNDED WEIGHTED COMPOSITION OPERATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 3 / December 2012
- Published online by Cambridge University Press:
- 09 April 2013, pp. 333-343
- Print publication:
- December 2012
-
- Article
-
- You have access
- Export citation
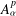
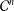
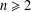
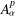
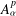
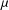

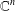
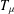
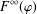
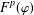
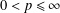

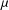
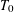
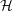
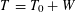
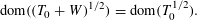
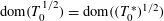
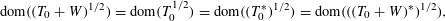
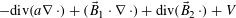
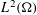
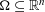
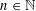
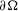
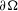
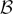
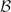
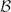
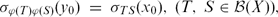
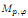 of sublinear operators generated by the parabolic Calderón—Zygmund operator and by the commutator of this operator with bounded mean oscillation (BMO) functions. As a consequence, we obtain a global
of sublinear operators generated by the parabolic Calderón—Zygmund operator and by the commutator of this operator with bounded mean oscillation (BMO) functions. As a consequence, we obtain a global 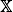 with transition kernel
with transition kernel 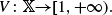 The Markov kernel
The Markov kernel 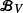 associated with
associated with 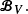 A general procedure to compute ρ
A general procedure to compute ρ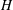
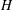
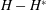
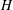

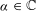
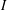
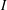

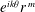
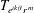



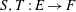
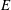
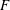
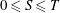
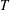

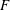

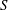

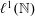
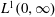
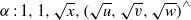
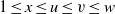
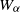


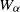
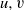
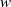
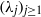
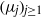
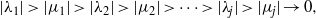
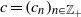
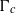
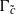
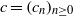
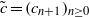
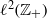
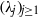
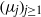

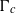
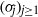
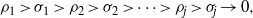
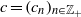
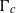
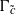
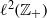
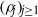
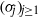
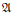 over the maximal ideal space of the centre of
over the maximal ideal space of the centre of