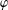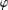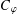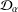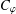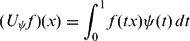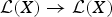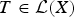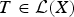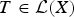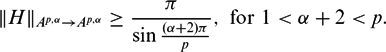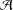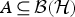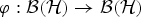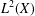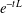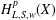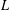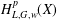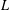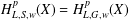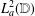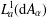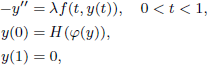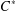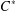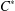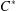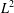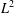Refine listing
Actions for selected content:
321 results in 47Bxx
Note on Spectra of Non-Selfadjoint Operators Over Dynamical Systems
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 15 February 2018, pp. 371-386
-
- Article
- Export citation
THE ESSENTIAL NORMS OF COMPOSITION OPERATORS ON WEIGHTED DIRICHLET SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 31 January 2018, pp. 297-307
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
GENERALIZED HARDY–CESÀRO OPERATORS BETWEEN WEIGHTED SPACES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 1 / January 2019
- Published online by Cambridge University Press:
- 28 January 2018, pp. 13-24
- Print publication:
- January 2019
-
- Article
-
- You have access
- Export citation
Linear Surjective Maps Preserving at Least One Element from the Local Spectrum
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 23 January 2018, pp. 169-175
-
- Article
- Export citation
AN EXTENSION OF THE BANACH–STONE THEOREM
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 105 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 08 November 2017, pp. 1-23
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
NORM OF THE HILBERT MATRIX OPERATOR ON THE WEIGHTED BERGMAN SPACES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 18 October 2017, pp. 513-525
- Print publication:
- September 2018
-
- Article
-
- You have access
- Export citation
From Hankel Operators to Carleson Measures in a Quaternionic Variable
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 17 July 2017, pp. 565-585
-
- Article
- Export citation
Quasi boundary triples and semi-bounded self-adjoint extensions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 5 / October 2017
- Published online by Cambridge University Press:
- 28 June 2017, pp. 895-916
- Print publication:
- October 2017
-
- Article
- Export citation
LIE
 $n$ -HIGHER DERIVATIONS AND LIE
$n$ -HIGHER DERIVATIONS AND LIE  $n$ -HIGHER DERIVABLE MAPPINGS
$n$ -HIGHER DERIVABLE MAPPINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 09 June 2017, pp. 223-232
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
OPERATING FUNCTIONS ON MODULATION AND WIENER AMALGAM SPACES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 230 / June 2018
- Published online by Cambridge University Press:
- 17 April 2017, pp. 72-82
- Print publication:
- June 2018
-
- Article
-
- You have access
- HTML
- Export citation
THE ROLE OF DOMINATION AND SMOOTHING CONDITIONS IN THE THEORY OF EVENTUALLY POSITIVE SEMIGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 29 March 2017, pp. 286-298
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
ON ∞-COMPLEX SYMMETRIC OPERATORS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 23 February 2017, pp. 35-50
- Print publication:
- January 2018
-
- Article
-
- You have access
- Export citation
On the Range Inclusion for Normal Derivations on C*-algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 22 February 2017, pp. 1-11
-
- Article
- Export citation
LITTLEWOOD–PALEY CHARACTERIZATION OF WEIGHTED HARDY SPACES ASSOCIATED WITH OPERATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 10 November 2016, pp. 250-267
- Print publication:
- October 2017
-
- Article
-
- You have access
- Export citation
FACTORIZATION OF OPERATORS THROUGH SUBSPACES OF
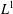 $L^{1}$ -SPACES
$L^{1}$ -SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 08 November 2016, pp. 313-328
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
THE HILBERT–SCHMIDT NORM OF A COMPOSITION OPERATOR ON THE BERGMAN SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 2 / April 2017
- Published online by Cambridge University Press:
- 02 November 2016, pp. 250-259
- Print publication:
- April 2017
-
- Article
-
- You have access
- Export citation
On Semipositone Non-Local Boundary-Value Problems with Nonlinear or Affine Boundary Conditions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 3 / August 2017
- Published online by Cambridge University Press:
- 02 November 2016, pp. 635-649
-
- Article
- Export citation
A CHARACTERISATION OF CENTRAL ELEMENTS IN
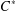 $C^{\ast }$ -ALGEBRAS
$C^{\ast }$ -ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 19 October 2016, pp. 138-143
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
THE MODIFIED QUANTUM WIGNER SYSTEM IN WEIGHTED
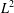 $L^{2}$ -SPACE
$L^{2}$ -SPACE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 13 October 2016, pp. 73-83
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
Computable bounds of an 𝓁²-spectral gap for discrete Markov chains with band transition matrices
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 53 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 24 October 2016, pp. 946-952
- Print publication:
- September 2016
-
- Article
- Export citation