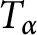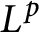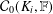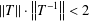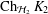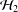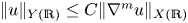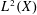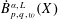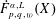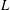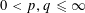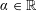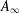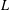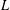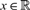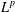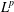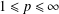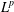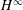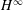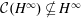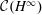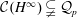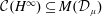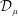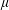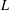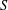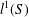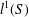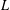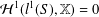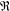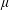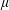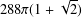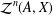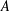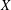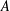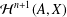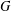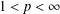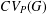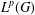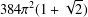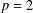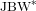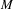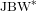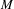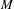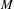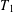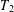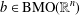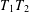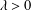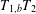Refine listing
Actions for selected content:
321 results in 47Bxx
Complete boundedness of multiple operator integrals
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 27 July 2020, pp. 474-490
- Print publication:
- June 2021
-
- Article
- Export citation
Growth of frequently hypercyclic functions for some weighted Taylor shifts on the unit disc
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 11 June 2020, pp. 264-281
- Print publication:
- June 2021
-
- Article
- Export citation
SMALL-BOUND ISOMORPHISMS OF FUNCTION SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 111 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 18 March 2020, pp. 412-429
- Print publication:
- December 2021
-
- Article
- Export citation
Embeddings of homogeneous Sobolev spaces on the entire space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 09 March 2020, pp. 296-328
- Print publication:
- February 2021
-
- Article
- Export citation
WEIGHTED BESOV AND TRIEBEL–LIZORKIN SPACES ASSOCIATED WITH OPERATORS AND APPLICATIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 26 February 2020, e11
-
- Article
-
- You have access
- Open access
- Export citation
Spectral projections correlation structure for short-to-long range dependent processes
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 31 January 2020, pp. 1-31
-
- Article
- Export citation
COMPACT WEIGHTED COMPOSITION OPERATORS BETWEEN
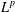 $L^{p}$-SPACES
$L^{p}$-SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 16 January 2020, pp. 151-161
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
The Range of the Cesàro Operator Acting on
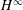 $H^{\infty }$
$H^{\infty }$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 04 December 2019, pp. 633-642
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
Fredholm Toeplitz operators with VMO symbols and the duality of generalized Fock spaces with small exponents
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 02 December 2019, pp. 3163-3186
- Print publication:
- December 2020
-
- Article
-
- You have access
- Open access
- Export citation
POWERS OF COMPOSITION OPERATORS: ASYMPTOTIC BEHAVIOUR ON BERGMAN, DIRICHLET AND BLOCH SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 108 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 27 November 2019, pp. 289-320
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
THE FIRST COHOMOLOGY GROUP OF BANACH INVERSE SEMIGROUP ALGEBRAS WITH COEFFICIENTS IN
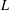 $L$-EMBEDDED BANACH BIMODULES
$L$-EMBEDDED BANACH BIMODULES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 16 September 2019, pp. 488-495
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
GENERALIZED JORDAN DERIVATIONS ON SEMIPRIME RINGS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 29 July 2019, pp. 36-43
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Embedding Theorems for Dirichlet Type Spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 22 July 2019, pp. 106-117
- Print publication:
- March 2020
-
- Article
-
- You have access
- Export citation
A Measurable Selector in Kadison’s Carpenter’s Theorem
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 16 July 2019, pp. 1505-1528
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
Toeplitz operators on Bergman spaces of polygonal domains
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 4 / November 2019
- Published online by Cambridge University Press:
- 26 June 2019, pp. 1115-1136
-
- Article
- Export citation
A priori bounds and existence of non-real eigenvalues for singular indefinite Sturm–Liouville problems with limit-circle type endpoints
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 07 June 2019, pp. 2607-2619
- Print publication:
- October 2020
-
- Article
- Export citation
HYPERREFLEXIVITY CONSTANTS OF THE BOUNDED
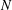 $N$-COCYCLE SPACES OF GROUP ALGEBRAS AND C*-ALGEBRAS
$N$-COCYCLE SPACES OF GROUP ALGEBRAS AND C*-ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 30 April 2019, pp. 112-130
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Effective multi-scale approach to the Schrödinger cocycle over a skew-shift base
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 10 / October 2020
- Published online by Cambridge University Press:
- 17 April 2019, pp. 2788-2853
- Print publication:
- October 2020
-
- Article
- Export citation
ON THE EXTENSION OF ISOMETRIES BETWEEN THE UNIT SPHERES OF A
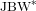 $\text{JBW}^{\ast }$-TRIPLE AND A BANACH SPACE
$\text{JBW}^{\ast }$-TRIPLE AND A BANACH SPACE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 15 April 2019, pp. 277-303
- Print publication:
- January 2021
-
- Article
- Export citation
WEIGHTED WEAK TYPE ENDPOINT ESTIMATES FOR THE COMPOSITIONS OF CALDERÓN–ZYGMUND OPERATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 109 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 08 April 2019, pp. 320-339
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation