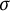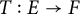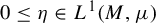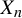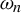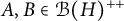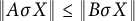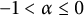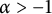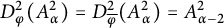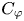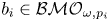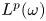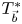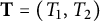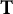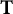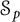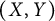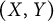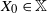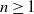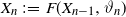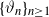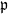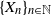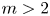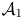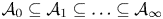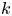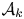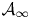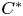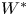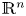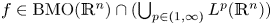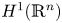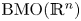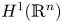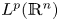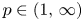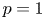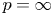Refine listing
Actions for selected content:
321 results in 47Bxx
Some results on various types of compactness of weak* Dunford–Pettis operators on Banach lattices
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 23 October 2023, pp. 403-414
- Print publication:
- June 2024
-
- Article
- Export citation
On the quasi-ergodicity of absorbing Markov chains with unbounded transition densities, including random logistic maps with escape
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 25 September 2023, pp. 1818-1855
- Print publication:
- July 2024
-
- Article
- Export citation
Every symmetric Kubo–Ando connection has the order-determining property
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 11 September 2023, pp. 279-288
- Print publication:
- June 2024
-
- Article
- Export citation
Order continuity of Arens extensions of regular multilinear operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 11 September 2023, pp. 258-279
- Print publication:
- February 2025
-
- Article
- Export citation
Sub-Bergman Hilbert spaces on the unit disk III
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 22 August 2023, pp. 1520-1537
- Print publication:
- October 2024
-
- Article
- Export citation
Toeplitz determinants with a one-cut regular potential and Fisher–Hartwig singularities I. Equilibrium measure supported on the unit circle
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 15 August 2023, pp. 1431-1472
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Schatten class composition operators on the Hardy space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 24 July 2023, pp. 1364-1377
- Print publication:
- October 2024
-
- Article
- Export citation
Uncertainty principles in holomorphic function spaces on the unit ball
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 10 July 2023, pp. 122-136
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The commutators of multilinear Calderón–Zygmund operators on weighted Hardy spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 26 June 2023, pp. 1259-1280
- Print publication:
- August 2024
-
- Article
- Export citation
TROTTER–KATO PRODUCT FORMULA AND AN APPROXIMATION FORMULA FOR A PROPAGATOR IN SYMMETRIC OPERATOR IDEALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 16 June 2023, pp. 173-174
- Print publication:
- August 2023
-
- Article
-
- You have access
- HTML
- Export citation
Nontrivial invariant subspaces of linear operator pencils
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 07 June 2023, pp. 1-8
- Print publication:
- March 2024
-
- Article
- Export citation
Linear preservers on idempotents of Fourier algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 17 May 2023, pp. 1326-1340
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Composition operators on weighted analytic spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 17 April 2023, pp. 1213-1230
- Print publication:
- December 2023
-
- Article
- Export citation
General Toeplitz kernels and
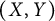 $(X,Y)$-invariance
$(X,Y)$-invariance
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 27 March 2023, pp. 680-706
- Print publication:
- April 2024
-
- Article
- Export citation
Robustness of iterated function systems of Lipschitz maps
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 28 February 2023, pp. 921-944
- Print publication:
- September 2023
-
- Article
- Export citation
On a class of difference operator and its applications to a family of analytic functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 27 February 2023, pp. 248-258
- Print publication:
- February 2024
-
- Article
- Export citation
Weakly concave operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 18 January 2023, pp. 1-32
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Square roots of weighted shifts of multiplicity two
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 23 December 2022, pp. 791-807
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On BMO and Hardy regularity estimates for a class of non-local elliptic equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 14 December 2022, pp. 2025-2052
- Print publication:
- December 2023
-
- Article
- Export citation
On a class of Hilbert-type inequalities in the whole plane involving some classical kernel functions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 3 / August 2022
- Published online by Cambridge University Press:
- 06 October 2022, pp. 833-846
-
- Article
- Export citation